Simple Linear Regression

Task 1: Getting to know the data

  1. 데이터를 여기에서 다운로드해서 grades로 저장하시오.
    힌트: haven 라이브러리의 read_dta 함수 사용해서 .dta 형식의 파일 불러오면 됨. (참고: .dta는 Stata에서 사용하는 데이터 파일 확장자임.)
library(haven)
link <- "https://raw.githack.com/chung-jiwoong/FMB819-Slides/refs/heads/main/chapter_slr/data/grade5.dta"
grades <- read_dta(link)

  1. 데이터셋 설명:

    • 관측 단위는? 즉, 각 행이 무엇을 의미하는가?
    • 총 몇 개의 관측치가 있는가?
    • 데이터셋을 확인하고 어떤 변수가 있는지 확인하시오. avgmath와 avgverb는 뭘 의미하는가?
    • skimr 패키지의 skim 함수 사용해서 classize, avgmath, avgverb 변수에 대한 기본적인 요약 통계 확인함.
      힌트: dplyr의 select 사용해서 변수 선택한 후 %>%로 skim() 적용하면 됨.
nrow(grades)
## [1] 2019
names(grades)
## [1] "schlcode"          "school_enrollment" "grade"            
## [4] "classize"          "avgmath"           "avgverb"          
## [7] "disadvantaged"     "female"            "religious"

avgmath: 학급의 평균 수학 점수 avgverb: 학급의 평균 언어 점수

if (!require("skimr")) install.packages("skimr")

library(skimr)
library(tidyverse)

grades %>%
    select(classize, avgmath, avgverb) %>%
    skim()
Data summary
Name Piped data
Number of rows 2019
Number of columns 3
_______________________
Column type frequency:
numeric 3
________________________
Group variables None

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
classize 0 1 29.93 6.56 5.00 26.00 31.00 35.00 44.00 ▁▁▆▇▃
avgmath 0 1 67.30 9.60 27.69 61.12 67.82 74.08 93.93 ▁▂▇▇▁
avgverb 0 1 74.38 7.68 34.80 69.83 75.38 79.84 93.86 ▁▁▃▇▂

skim 함수는 변수에 대한 몇 가지 유용한 통계를 제공합니다. 반 크기와 평균 점수 변수에는 결측값이 없습니다. 반 크기는 최소 5명에서 최대 44명까지 분포하며, 평균적으로 약 30명입니다. 작은 반의 수는 비교적 적으며, 25번째 백분위수(1사분위수)는 26명입니다. 또한 평균 수학 점수가 평균 언어 점수보다 약간 낮았으며, 수학 점수의 분포가 언어 점수보다 더 넓게 퍼져 있음을 알 수 있습니다.

  1. 학급 규모와 학생 성취도 간 실제 (선형) 관계에 대해 어떤 관계가 있을 것이라 생각하는가?

한편으로는, 작은 반에서는 개별화된 학습이 더 용이할 수 있으며, 교사들이 성취도가 낮은 학생들을 더 쉽게 모니터링할 수 있습니다. 그러나 교사들이 작은 반의 장점을 충분히 활용할 수 있도록 훈련되지 않았다면, 작은 반이 반드시 유익하지 않을 수도 있습니다.

또한, 국가에 따라 작은 반이 경제적으로 열악한 지역에서 더 흔할 수 있으며, 이 경우 반 크기와 학생 성취도 사이에 양의 관계가 나타날 수 있습니다. 반대로, 보다 신중한 부모들은 작은 반이 자녀에게 더 유리할 것이라고 생각하여 반 크기가 작은 지역으로 이사할 가능성이 높으며, 이 경우 반 크기와 학생 성취도 사이에 음의 관계가 나타날 가능성이 큽니다.

산점도를 사용하면 반 크기와 학생 성취도 간의 관계를 처음으로 탐색하는 데 도움이 될 것입니다.

# cowplot 패키지 로드 (ggplot2 그래프를 결합하기 위해 사용)
library(cowplot)

# 첫 번째 산점도: 반 크기(classize)와 평균 언어 점수(avgverb)의 관계
scatter_verb <- grades %>%
    ggplot() +  # ggplot 객체 생성
    aes(x = classize, y = avgverb) +  # x축: 반 크기, y축: 평균 언어 점수
    geom_point() +  # 산점도 추가
    scale_x_continuous(limits = c(0, 45), breaks = seq(0, 45, 5)) +  # x축 범위를 0~45로 설정하고 5 단위로 눈금 추가
    scale_y_continuous(limits = c(0, 100), breaks = seq(0, 100, 20)) +  # y축 범위를 0~100으로 설정하고 20 단위로 눈금 추가
    labs(x = "Class size",  # x축 라벨 설정
         y = "Average reading score")  # y축 라벨 설정

# 두 번째 산점도: 반 크기(classize)와 평균 수학 점수(avgmath)의 관계
scatter_math <- grades %>%
    ggplot() +  # ggplot 객체 생성
    aes(x = classize, y = avgmath) +  # x축: 반 크기, y축: 평균 수학 점수
    geom_point() +  # 산점도 추가
    scale_x_continuous(limits = c(0, 45), breaks = seq(0, 45, 5)) +  # x축 범위를 0~45로 설정하고 5 단위로 눈금 추가
    scale_y_continuous(limits = c(0, 100), breaks = seq(0, 100, 20)) +  # y축 범위를 0~100으로 설정하고 20 단위로 눈금 추가
    labs(x = "Class size",  # x축 라벨 설정
         y = "Average math score")  # y축 라벨 설정

# cowplot의 plot_grid()를 사용하여 두 개의 산점도를 하나의 플롯으로 결합
plot_grid(scatter_verb, scatter_math, labels = c("Reading", "Mathematics"))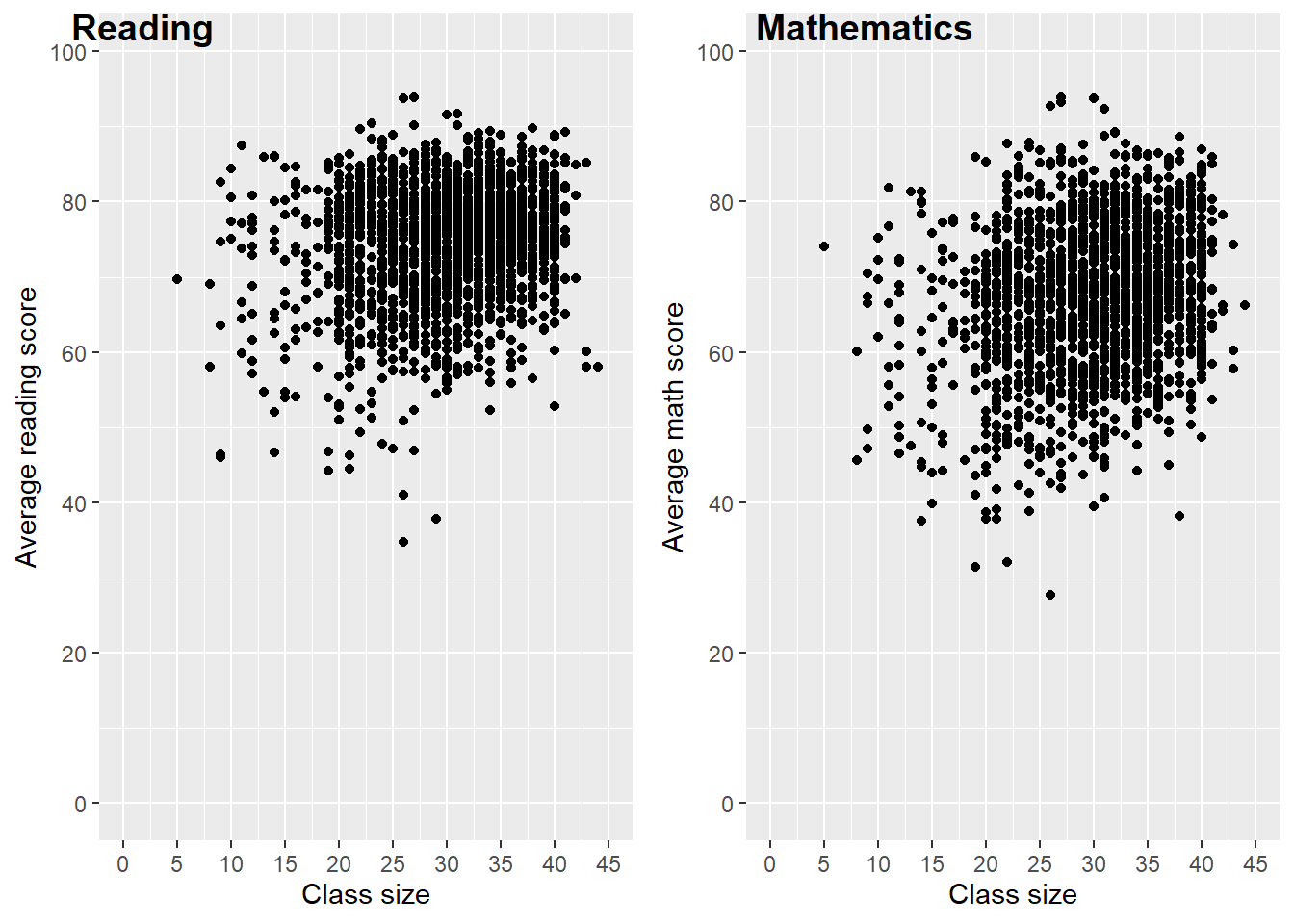

# labels 옵션을 사용하여 각각의 플롯에 "Reading"과 "Mathematics"라는 레이블 추가
  1. 학급 규모와 수학/언어 점수 간 상관관계는?
grades %>%
    summarise(cor_verb = cor(classize, avgverb),
             cor_math = cor(classize, avgmath))
## # A tibble: 1 × 2
##   cor_verb cor_math
##      <dbl>    <dbl>
## 1    0.190    0.217

두 상관계수는 양수이며, 이는 이전 산점도에서 관찰된 양의 상관관계와 일치합니다. 그러나 상관계수는 약 0.2로 상당히 낮아, 관계가 그리 강하지 않음을 시사합니다.

상관계수가 1이면 완전한 양의 선형 관계를 의미하며, 즉 모든 점이 동일한 직선 위에 놓이게 됩니다. 반대로, 상관계수가 -1이면 완전한 음의 선형 관계를 의미합니다. 상관계수가 0이면 선형적인 관계가 전혀 없음을 뜻합니다.

Task 2: OLS Regression

다음 코드를 실행하여 데이터를 학급 규모(class size) 수준에서 집계하시오:

grades_avg_cs <- grades %>%
  group_by(classize) %>%
  summarise(avgmath_cs = mean(avgmath),
            avgverb_cs = mean(avgverb))
  1. 평균 언어 점수(avgverb_cs)를 학급 규모(classize)에 대해 회귀분석 수행. 회귀 계수(coefficients)를 해석하시오.
lm(avgverb_cs ~ classize, grades_avg_cs)
## 
## Call:
## lm(formula = avgverb_cs ~ classize, data = grades_avg_cs)
## 
## Coefficients:
## (Intercept)     classize  
##     69.1861       0.1332

( b_0 ) (절편)의 해석: 반 크기가 0명일 때 예측된 평균 언어 점수는 69.19입니다. 하지만 이는 현실적으로 의미가 없습니다. 왜냐하면 반에 학생이 한 명도 없다면 점수도 존재할 수 없기 때문입니다. 따라서 표본 외 예측 (out-of-sample predictions), 즉 데이터 범위를 벗어난 값에 대한 예측에는 주의해야 합니다.

( b_1 ) (기울기)의 해석: 평균적으로, 반 크기가 학생 1명 증가할 때 평균 언어 점수가 0.13만큼 증가하는 것으로 나타났습니다.

  1. 이 회귀분석에서 OLS 계수 \(b_0\) 및 \(b_1\)을 직접 계산 (공식 이용).
    힌트: cov, var, mean 함수 사용.
cov_x_y = grades_avg_cs %>%
    summarise(cov(classize, avgmath_cs))
var_x = var(grades_avg_cs$classize)
b_1 = cov_x_y / var_x
b_1
##   cov(classize, avgmath_cs)
## 1                  0.191271
y_bar = mean(grades_avg_cs$avgmath_cs)
x_bar = mean(grades_avg_cs$classize)
b_0 = y_bar - b_1 * x_bar
b_0
##   cov(classize, avgmath_cs)
## 1                  61.10917
  1. 학급 규모가 0일 때, 예측된 평균 언어 점수는 얼마인가? 이 값이 실제로 의미가 있는가?

기울기 계수 \(b_1\) 는 평균 수학 점수에서 얻은 계수와 매우 유사합니다. 이는 예상된 결과인데, 두 점수에 대한 산점도가 서로 비슷한 패턴을 보였기 때문입니다.

  1. 학급 규모가 30명일 때, 예측된 평균 언어 점수는 얼마인가?

반 크기가 30명일 때의 예측된 평균 언어 점수는 다음과 같습니다: \(69.19 + 0.13 \times 30 = 73.09\)

Task 3: \(R^2\) and goodness of fit

  1. avgmath_cs를 classize에 대해 회귀(regress)하고 결과를 math_reg 객체에 저장.
math_reg <- lm(avgmath_cs ~ classize, grades_avg_cs)
  1. summary(math_reg)를 실행하여 (다중) \(R^2\) 값을 확인함. 이 값의 의미를 해석할 것.
summary(math_reg)
## 
## Call:
## lm(formula = avgmath_cs ~ classize, data = grades_avg_cs)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9.7543 -1.7985  0.3109  1.4768 11.9345 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 61.10917    1.43598  42.556  < 2e-16 ***
## classize     0.19127    0.05175   3.696 0.000725 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.528 on 36 degrees of freedom
## Multiple R-squared:  0.2751, Adjusted R-squared:  0.2549 
## F-statistic: 13.66 on 1 and 36 DF,  p-value: 0.0007249

\(R^2\) 값은 약 0.28로, 이는 평균 수학 점수의 변동성 중 약 28%가 반 크기에 의해 설명된다는 것을 의미합니다.

  1. classize와 avgmath_cs 간 상관계수(correlation)를 제곱하여 계산. 이 값은 단일 설명변수(one regressor)를 가진 회귀에서 \(R^2\)와 상관계수 간의 관계를 보여줌을 보이시오.
grades_avg_cs %>%
  summarise(cor_sq = cor(classize, avgmath_cs)^2)
## # A tibble: 1 × 1
##   cor_sq
##    <dbl>
## 1  0.275

단 하나의 독립 변수를 가진 회귀 분석에서는 ( R^2 ) 값이 종속 변수와 독립 변수 간의 상관계수의 제곱과 동일합니다.

  1. 1번과 2번을 avgverb_cs에 대해 반복. 어떤 시험에서 학급 규모의 분산이 학생 점수의 분산을 더 많이 설명하는지 비교하시오.
verb_reg <- lm(avgverb_cs ~ classize, grades_avg_cs)
summary(verb_reg)
## 
## Call:
## lm(formula = avgverb_cs ~ classize, data = grades_avg_cs)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -17.0152  -0.2451   0.8818   1.8443   8.8323 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 69.18610    1.69180  40.895   <2e-16 ***
## classize     0.13316    0.06097   2.184   0.0356 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.157 on 36 degrees of freedom
## Multiple R-squared:  0.117,  Adjusted R-squared:  0.09246 
## F-statistic:  4.77 on 1 and 36 DF,  p-value: 0.03557

( R^2 ) 값이 수학 점수에서 더 크므로, 반 크기가 읽기 점수보다 수학 점수의 변동성을 더 많이 설명한다는 것을 의미합니다.

  1. (Optional) broom 패키지를 설치 및 로드한 후, math_reg를 augment() 함수에 전달하여 새로운 객체에 저장함.
    avgmath_cs의 분산(SST)과 예측값 .fitted의 분산(SSE)을 사용하여 \(R^2\) 값을 직접 계산하시오. (이전 슬라이드의 공식을 참고할 것.)
if (!require("bloom")) install.packages("bloom", dependencies=TRUE, repos = "https://cloud.r-project.org/")

library(broom)

math_reg_aug <- augment(math_reg)
SST = var(grades_avg_cs$avgmath_cs)
SSE = var(math_reg_aug$.fitted)
SSE/SST
## [1] 0.275055