Regression Inference

FMB819: R을 이용한 데이터분석

고려대학교 경영대학 정지웅

Today’s Agenda

• 회귀 테이블 (regression table) 이해하기

• 이론 기반 (theory-based) vs. 시뮬레이션 기반 (simulation-based) 추론 비교

• 고전적 회귀 모델 (Classical Regression Model) 가정

• 실증적 응용 사례:

  • 학급 크기와 학생 성취도
  • 성별에 따른 교육의 수익률

학급 크기와 학생 성취도

• STAR 실험 데이터를 다시 살펴보자:

  • 소규모 학급 (small) 과 일반 학급 (regular)
  • 유치원 (Kindergarten) 학년

• 다음 회귀 모델을 고려하고 OLS로 추정:

\[ \text{math score}_i = b_0 + b_1 \text{small}_i + e_i\]

library(tidyverse)

star_df = read.csv("https://www.dropbox.com/s/bf1fog8yasw3wjj/star_data.csv?dl=1")
star_df = star_df[complete.cases(star_df),]
star_df = star_df %>%
  filter(star %in% c("small","regular") &
           grade == "k") %>% 
  mutate(small = (star == "small"))

reg_star = lm(math ~ small, star_df)
reg_star

Call:
lm(formula = math ~ small, data = star_df)

Coefficients:
(Intercept)    smallTRUE  
    484.446        8.895  

• 테네시에서 다른 무작위 표본을 선택하여 실험을 다시 수행하면, \(b_1\) 값이 다르게 나올까?

• 답은 Yes, 하지만 이 추정값이 얼마나 다르게 나올 가능성이 있을까?

회귀 추론: \(b_k\) vs \(\beta_k\)

• \(b_0, b_1\) 는 우리가 표본에서 계산한 점 추정치 (point estimates) 임.

  • 마치 파스타 예제에서 본 표본 비율 \(\hat{p}\) 과 같음!

• 사실, 우리가 추정한 모델은…

\[\hat{y} = b_0 + b_1 x_1\]

… 알 수 없는 진짜 모집단 회귀선에 대한 추정치임.

\[y = \beta_0 + \beta_1 x_1\]

여기서 \(\beta_0, \beta_1\) 는 관심 있는 모집단 모수 (population parameters) 임.

• 보통 \(b_k\) 대신 \(\hat{\beta_k}\) 를 사용하기도 하며, 둘 다 \(\beta_k\) 에 대한 표본 추정치를 의미함.

• 이제 우리가 배운 신뢰구간 (confidence intervals), 가설검정 (hypothesis testing), 그리고 표준오차 (standard errors) 를 활용하여 \(\hat{\beta_k}\) 에 적용해 보겠음!

회귀 테이블 이해하기

• 다음은 tidy 처리된 회귀 결과임:

# A tibble: 2 × 5
  term        estimate std.error statistic     p.value
  <chr>          <dbl>     <dbl>     <dbl>       <dbl>
1 (Intercept)   484.        1.15    421.   0          
2 smallTRUE       8.90      1.68      5.30 0.000000123

• 여기서 새로운 3개의 열이 추가됨: std.error, statistic, p.value.

Entry	Meaning
std. error	\(b_k\) 의 표준오차 (standard error)
statistic	귀무가설 \(H_0:\beta_k = 0\) vs 대립가설 \(H_A:\beta_k \neq 0\) 에 대한 검정 통계량
p.value	귀무가설 \(H_0:\beta_k = 0\) vs 대립가설 \(H_A:\beta_k \neq 0\) 에 대한 p-값

• small 변수의 계수를 중심으로 각각의 항목을 이해해보자.

\(b_k\)의 표준 오차 (Standard Error)

\(b_k\)의 표준 오차 (Standard Error of \(b_k\)): \(b_k\)의 샘플링 분포의 표준 편차.

우리가 실험을 1,000번 반복하고, 1,000개의 서로 다른 표본을 사용할 수 있다고 가정하자:

• 그러면 1,000개의 회귀분석을 실행하고, \(\beta_k\)에 대한 1,000개의 추정치 \(b_k\)를 얻게 됨.

• \(b_k\)의 표준 오차는 (무한히 많은) 표본에서 \(b_k\)가 얼마나 변동할지를 정량화함.

\(b_\textrm{small}\)의 표준 오차 (Standard Error)

• 회귀 테이블에서 얻은 값: \(\hat{\textrm{SE}}(b_\textrm{small}) = 1.68\)

  • 여기서 \(\hat{\textrm{SE}}\)를 사용한 이유는, 우리가 얻은 1.68 값이 표본에서 추정된 표준 오차이기 때문임. 실제 표준 오차는 \({\textrm{SE}}\)로 표현됨.

  • 실제 표준 오차 \({\textrm{SE}}\)를 알고 싶지만, 우리는 단 하나의 표본만 가지고 있음!

• 이제 \(b_\textrm{small}\)의 샘플링 분포를 시뮬레이션하여, 표준 오차가 어떻게 계산되는지 확인해 보자.

Task 1

10:00

녹색 파스타 비율의 샘플링 분포를 생성한 것처럼, \(b_\textrm{small}\)의 부트스트랩 분포를 생성하자.

1. 학급 크기와 학생 성취도 슬라이드(링크)에서 데이터 로딩 및 정리 코드**를 복사하여 실행.

2. star_df에서 1,000개의 샘플을 추출하여 \(b_\textrm{small}\)의 부트스트랩 분포를 생성하시오. 아래 코드를 사용하면 됨:

library(infer)
bootstrap_distrib <- star_df %>% 
    mutate(small=as.numeric(small)) %>% 
    specify(response = math, explanatory = small) %>%
    generate(reps = 1000, type = "bootstrap") %>%
    calculate(stat = "slope")

3. 이 시뮬레이션된 샘플링 분포를 시각화하고, \(b_\textrm{small}\)의 평균과 표준 오차를 계산하시오.

부트스트랩 분포

표준 오차 (Standard error): 1.63 \(\rightarrow\) 테이블의 값 (1.68)과 매우 유사함!

• 정확히 일치하지 않는 이유는 R이 사용하는 이론적 접근법 대신 부트스트랩 (시뮬레이션) 방법을 사용했기 때문임.

회귀분석 결과 다시 확인

library(broom)
tidy(lm(math ~ small, star_df))

# A tibble: 2 × 5
  term        estimate std.error statistic     p.value
  <chr>          <dbl>     <dbl>     <dbl>       <dbl>
1 (Intercept)   484.        1.15    421.   0          
2 smallTRUE       8.90      1.68      5.30 0.000000123

• std.error 열의 의미를 이해했음.

• 위에서 다음 두 개의 열은 statistic과 p.value임.

• 이전 수업에서 가설 검정 (hypothesis testing)에 대해 배웠음.

• 하지만 이 값들은 어떤 가설 검정에 해당하는 것일까?

\(\beta_k = 0\) vs \(\beta_k \neq 0\) 검정

• 기본적으로 회귀 분석 출력은 다음과 같은 가설 검정 결과를 제공함:

\[\begin{align}H_0:& \beta_k = 0\\H_A:& \beta_k \neq 0\end{align}\]

• 이를 통해 종속 변수(결과 변수)와 독립 변수(설명 변수) 간에 실제 관계가 있는지 통계적으로 검정할 수 있음.

• 만약 \(H_0\)이 참이라면, 종속 변수와 독립 변수 간에 관계가 없음.

  • 이 경우 \(b_1 \neq 0\)을 관측한 것은 단순한 우연일 가능성이 있음.

• 만약 \(H_0\)이 거짓이라면, 두 변수 사이에 실제 관계가 있음.

• 중요: 이 검정은 양측 검정 (two-sided test)임!

검정 통계량과 p-값

• 이미 살펴보았듯이, 가설 검정을 수행하려면 다음을 수행해야 함:

  • 검정 통계량 (statistic)의 표본 분포를 유도하여 귀무 가설 \(H_0\)이 참일 때의 귀무 분포를 생성함.

  • 관측된 검정 통계량이 이 가상의 세계에서 얼마나 극단적인지를 정량화함.

• 관측된 검정 통계량 (statistic)은 \(\frac{b}{\hat{SE}(b)}\)로 계산됨.

  • 왜 단순히 \(b\)가 아니라 이 공식을 사용하는가? 나중에 이에 대해 설명할 예정.

observed_stat = reg_star$coefficients[2]/sd(bootstrap_distrib$stat)
round(observed_stat,2)

smallTRUE 
     5.45 

• 표에서 얻은 검정 통계량 statistic = 5.3과 매우 유사함.: .

• p-값은 귀무 분포에서 \(\pm\) 관측된 검정 통계량 바깥쪽의 면적을 측정함.

• 마지막으로, 일반적인 유의 수준 \(\alpha\) = 0.1, 0.05, 0.01에서 \(H_0\)을 기각할 수 있는지 확인함.

\(\beta_\textrm{small} = 0\) vs \(\beta_\textrm{small} \neq 0\) 검정

• \(\frac{b_\textrm{small}}{\hat{SE}(b_\textrm{small})}\)의 귀무 분포(null distribution)를 시뮬레이션을 통해 근사화할 것임.

• 만약 수학 점수와 학급 크기 사이에 관계가 없다면, 즉 \(H_0\)가 참이고 \(\beta_\textrm{small} = 0\)이라면, small 값을 학생들 사이에서 재배열(reshuffling) / 순열(permuting) 하더라도 결과에 영향을 주지 않아야 함.

• 1,000개의 순열된 샘플 생성 및 \(b_\textrm{small}\) 계산

null_distribution <- star_df %>% 
  mutate(small=as.numeric(small)) %>% 
  specify(formula = math ~ small) %>%
  hypothesize(null = "independence") %>% 
  generate(reps = 1000, type = "permute") %>% 
  calculate(stat = "slope")

• 귀무 가설 하에서 검정 통계량 \(\frac{b_\textrm{small}}{\hat{SE}(b_\textrm{small})}\) 계산

null_distribution <- null_distribution %>%
  mutate(test_stat = stat/sd(bootstrap_distrib$stat))

• 부트스트랩 분포에서 \(\hat{SE}(b_\textrm{small})\) 값은 1.63로 계산되었음.

\(\beta_\textrm{small} = 0\) vs \(\beta_\textrm{small} \neq 0\) 검정

\(\beta_\textrm{small} = 0\) vs \(\beta_\textrm{small} \neq 0\) 검정

• 귀무 가설(\(H_0\))이 참일 때, \(b_\textrm{small}\) = 8.9 값을 얻을 확률은 매우 낮음.

\(\beta_\textrm{small} = 0\) vs \(\beta_\textrm{small} \neq 0\) 검정

• \(H_0\) 를 기각할지 여부를 결정하기 위해, 양측 검정을 고려해야 함.

• 즉, 더 극단적인 값이란 -5.447보다 작거나 또는 5.447보다 큰 경우를 의미함.

\(\beta_\textrm{small} = 0\) vs \(\beta_\textrm{small} \neq 0\) 검정

• p-value는?

\(\beta_\textrm{small} = 0\) vs \(\beta_\textrm{small} \neq 0\) 검정

• 귀무가설 (\(H_0\))을 기각할지 결정하려면, 양측 검정을 고려해야 함.
  더 극단적인 값이란 -5.45 이하이거나 5.45 이상을 의미함.

• p-값을 계산하면 다음과 같음:

p_value = mean(abs(null_distribution$test_stat) >= observed_stat)
p_value

[1] 0

• 이 값은 회귀 분석 표에 나오는 값과 동일함.

• 질문: 5% 유의수준에서 귀무가설을 기각할 수 있는가?

\(\beta_\textrm{small} = 0\) vs \(\beta_\textrm{small} \neq 0\) 검정

• 귀무가설 (\(H_0\))을 기각할지 결정하려면, 양측 검정을 고려해야 함.
  더 극단적인 값이란 -5.45 이하이거나 5.45 이상을 의미함.

• p-값을 계산하면 다음과 같음:

p_value = mean(abs(null_distribution$test_stat) >= observed_stat)
p_value

[1] 0

• 이 값은 회귀 분석 표에 나오는 값과 동일함.

• 답:

  • p-값이 0이므로, 어떤 유의수준에서도 (\(H_0\))를 기각할 수 있음.
    p-값은 항상 (\(\alpha\))보다 작음.

  • 다시 말해, (\(b_\textrm{small}\))은 어떤 유의수준에서도 0과 통계적으로 다름.

  • 또한 (\(b_\textrm{small}\))이 통계적으로 유의함 (어떤 유의수준에서도) 라고 할 수 있음.

Regression Inference: Theory

회귀 추론: 이론

• 지금까지는 시뮬레이션 기반 추론을 설명했음.

• 하지만 R의 통계 패키지에서 제공하는 값들은 이론적 방법으로 얻어진 것임.

• 이론적 추론은 대표본 근사를 기반으로 함.

  • 표본 분포가 적절한 분포로 수렴함을 보일 수 있음 ⟶ 중심극한정리

• 이제 이론 기반 접근법을 간단히 살펴보겠음.

회귀 추론: 이론

• 이론 기반 접근법 근간: 표본 통계량 \(\frac{b - \beta}{\hat{\textrm{SE}(b)}}\) 은 표본 크기가 커질수록 표준 정규 분포로 수렴함.

  • \(\hat{\textrm{SE}(b)}\) 는 \(b\) 의 표준편차에 대한 표본 추정량임.
  • 이 값은 이론적 공식을 통해 얻어짐 (링크에서 확인 가능) 하지만 여기서는 다루지 않겠음.

• 표준 정규 분포는 평균이 0이고 표준편차가 1인 정규 분포임.

• 여기서는 표본 분포를 시뮬레이션할 필요가 없음. 이론적으로 유도된 분포를 사용하여 신뢰구간을 구성하거나 가설 검정을 수행할 수 있음.

• 만약 \(\frac{b - \beta}{\hat{\textrm{SE}(b)}}\)가 표준 정규 분포로 수렴한다면, \(b\)는 평균이 \(\beta\)이고 표준편차가 \(\hat{\textrm{SE}(b)}\)인 정규 분포로 수렴함.

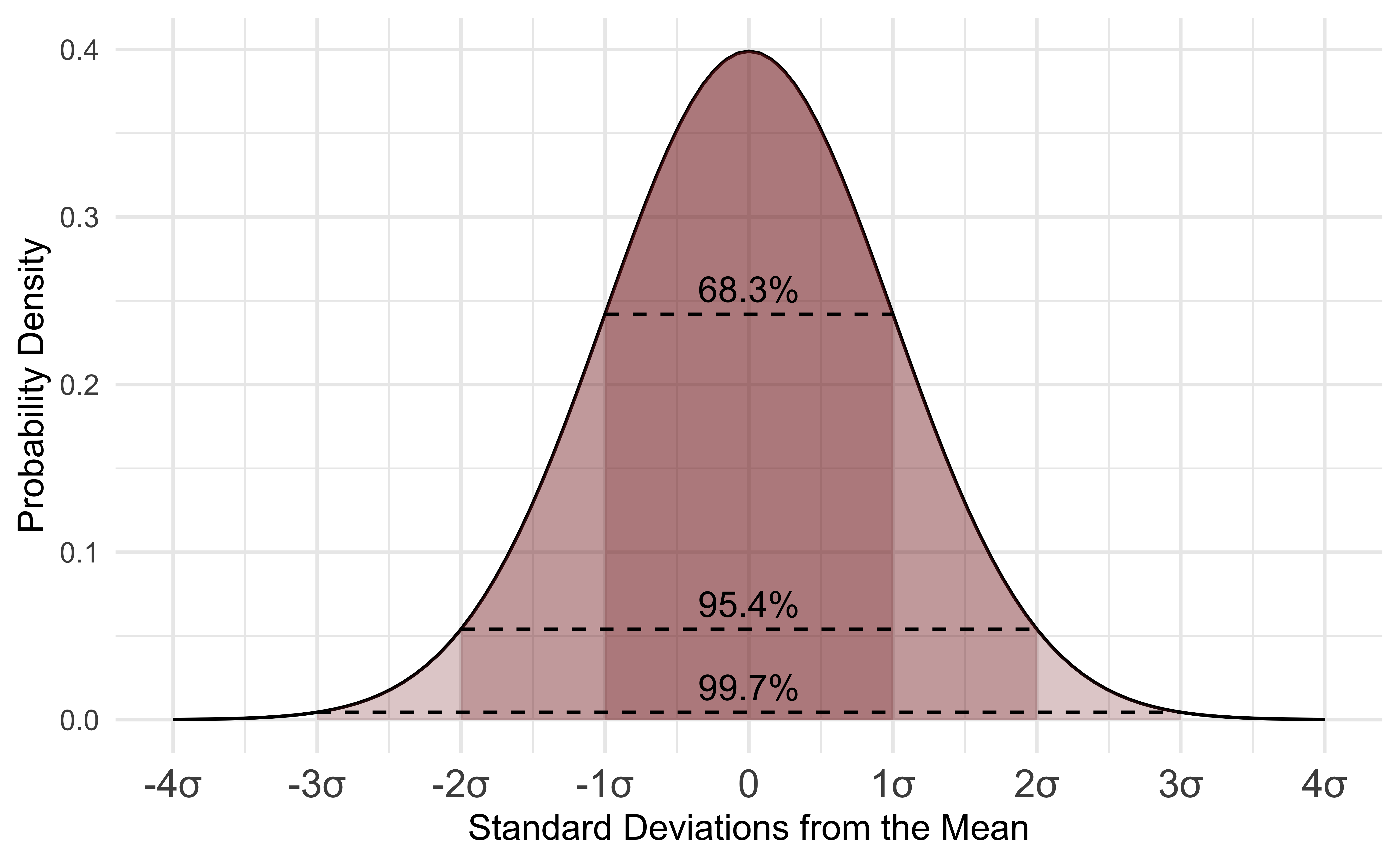
정규분포(Normal Distribution)

이론 기반 추론: 신뢰구간

• 95% 신뢰구간을 예로 들어보겠음.

• \(b\)의 표본 분포가 정규 분포를 따른다고 가정하면, 정규 분포에 대한 95% 근사 규칙을 적용할 수 있음.

• 정규 분포에서 95%의 값이 평균으로부터 약 2 표준편차(정확히는 1.96) 내에 존재함을 알고 있음.

• 따라서, \(\beta\)에 대한 95% 신뢰구간은 다음과 같이 계산할 수 있음:
  \[ \textrm{CI}_{95\%} = [ b \pm 1.96*\hat{\textrm{SE}}(b)] \]

tidy(lm(math ~ small, star_df),
     conf.int = TRUE, conf.level = 0.95) %>%
  filter(term == "smallTRUE") %>%
  select(term, conf.low, conf.high)

# A tibble: 1 × 3
  term      conf.low conf.high
  <chr>        <dbl>     <dbl>
1 smallTRUE     5.60      12.2

bootstrap_distrib %>%
  summarise(
    lower_bound = 8.895 - 1.96*sd(stat),
    upper_bound = 8.895 + 1.96*sd(stat))

# A tibble: 1 × 2
  lower_bound upper_bound
        <dbl>       <dbl>
1        5.69        12.1

• 적절한 정규 분포의 분위수를 사용하면, 이를 쉽게 임의의 신뢰수준으로 일반화할 수 있음.

Task 2

05:00

1. Task 1에서 생성한 부트스트랩 분포를 사용하여 퍼센타일 방법으로 95% 신뢰구간을 계산하시오.

2. 이전 슬라이드에서 구한 신뢰구간과 얼마나 유사한가?

신뢰구간: 시각화

이론 기반 추론: 가설 검정

• 이론적으로, \(\frac{b - \beta_k}{\hat{\textrm{SE}(b)}}\) 는 표준 정규 분포로 수렴함.

• 앞서 언급했듯이, 모든 통계 소프트웨어에서 기본적으로 수행하는 검정은 다음과 같음:

  \[ \begin{align} H_0:& \beta_k = 0 \\ H_A:& \beta_k \neq 0 \end{align} \]

• 따라서, 귀무가설 \(H_0\) 하에서 \(\beta_k=0\)이고, 이론적으로 표본 통계량 \(\frac{b}{\hat{\textrm{SE}(b)}}\) 의 분포가 표준 정규 분포를 따름.

• 즉, 표준 정규 분포가 검정 통계량의 귀무 분포가 됨.

• 해당 검정에 대한 p-값은 표준 정규 분포에서\(\pm\) 관측된 값 \(\frac{b}{\hat{\textrm{SE}(b)}}\) 바깥쪽 영역의 면적과 같음.

• 일반적인 기준: 추정값이 표준 오차의 두 배 이상이면 5% 유의수준에서 유의함. 왜 그런가?

회귀 분석 표 정리

• 이제 회귀 분석 표의 모든 구성 요소를 배웠으므로, 직접 생성하고 해석하는 방법을 익혀보겠음!

reg_simple_math <- lm(math ~ small, data=star_df)
reg_gender_math <- lm(math ~ small + gender , data=star_df)
reg_simple_read <- lm(read ~ small, data=star_df)
reg_gender_read <- lm(read ~ small + gender , data=star_df)

export_summs(reg_simple_math, reg_gender_math, reg_simple_read, reg_gender_read,
             model.names = c("Math score", "Math Score",
                             "Reading score", "Reading score"),
             coefs=c("Intercept" = "(Intercept)",
                     "Small class" = "smallTRUE",
                     "Male gender" = "gendermale"))

회귀 분석 표 정리

	Math score	Math Score	Reading score	Reading score
Intercept	484.45 ***	488.85 ***	435.76 ***	439.62 ***
	(1.15)	(1.43)	(0.75)	(0.93)
Small class	8.90 ***	8.94 ***	5.37 ***	5.41 ***
	(1.68)	(1.67)	(1.09)	(1.09)
Male gender		-8.56 ***		-7.49 ***
		(1.67)		(1.09)
N	3359	3359	3359	3359
R2	0.01	0.02	0.01	0.02
*** p < 0.001; ** p < 0.01; * p < 0.05.

회귀 분석 표 해석

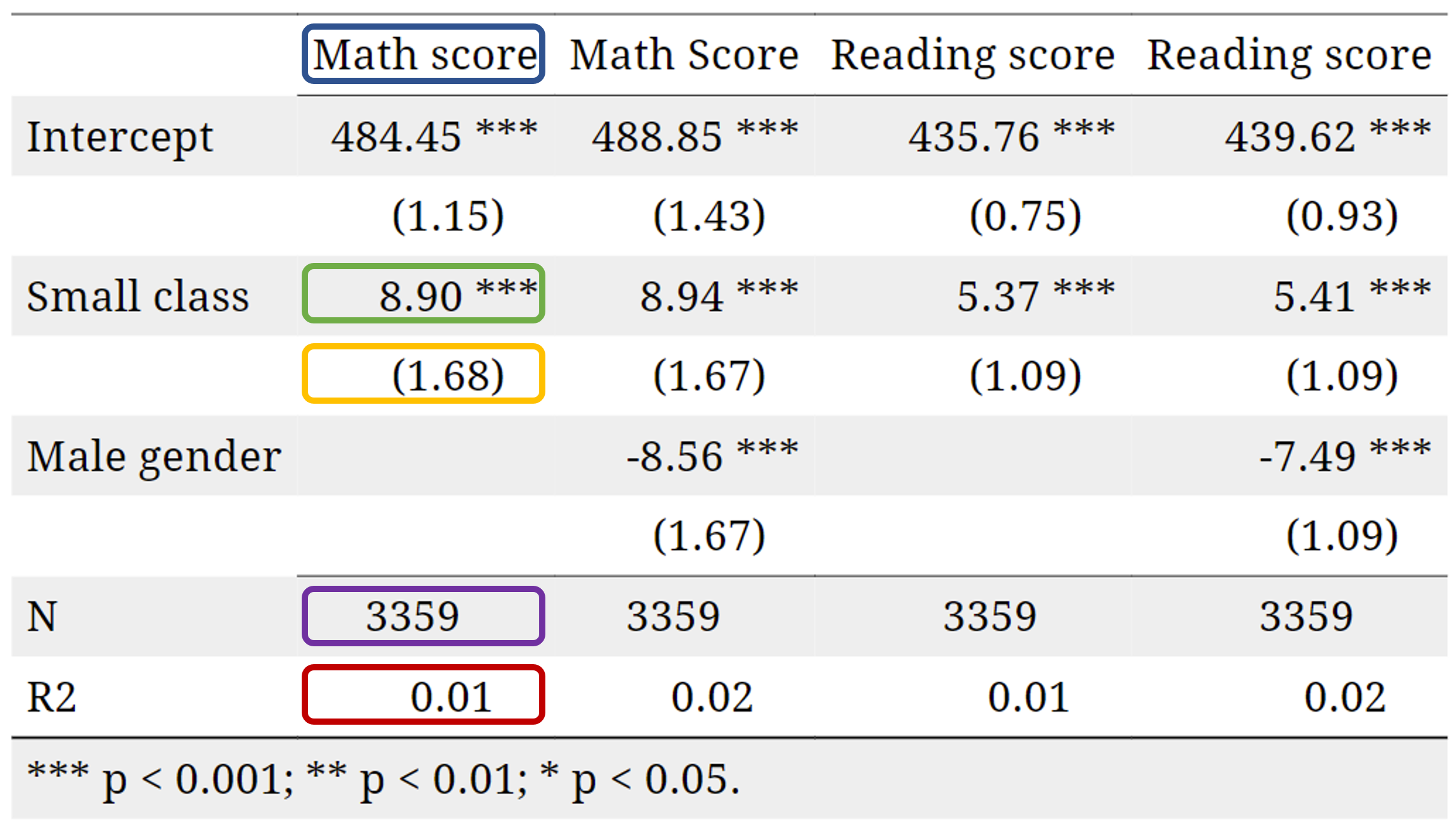
• 각 열은 하나의 회귀 분석을 나타냄. 첫 번째 회귀 분석에서 다음을 확인할 수 있음:

  • 결과 변수 이름: 파란색
  • 소규모 학급에 대한 추정 계수 \(\hat{\beta_\textrm{small}}\): 초록색
  • 추정된 표준 오차: 노란색
  • 관측치 수: 보라색
  • 결정계수 (\(R^2\)): 빨간색
  • 표 하단의 별(*)에 대한 해석

Classical Regression Model

고전적 회귀 모형 (CRM)

• 추론이 이론을 기반으로 하든 시뮬레이션을 기반으로 하든, 유효한 추론을 위해서는 몇 가지 가정이 충족되어야 함.

• 이러한 가정들을 만족하는 모형을 고전적 회귀 모형 (Classical Regression Model, CRM)이라고 함.

• 본격적으로 가정을 살펴보기 전에, 회귀 모형에 적용하는 몇 가지 작지만 중요한 수정 사항을 확인하겠음 ([단순선형회귀 강의] 참조).

• 이미 표본 추정량 \(b_k\) (또는 \(\hat{\beta_k}\))와 모집단 모수 \(\beta_k\)의 차이를 언급했음.

• 같은 방식으로, 표본 오차 (잔차, \(e\))와 모집단 모형의 오차항 \(\varepsilon\)을 구별해야 함.

  \[ y_i = \beta_0 + \beta_1 x_{1,i} + ... + \beta_k x_{k,i} + \varepsilon_i \]

• 고전적 회귀 모형은 올바르게 지정된 선형 회귀에 적용됨. 즉,

  • 모형은 계수에 대해 선형적이어야 하며,
    
  • 모든 관련 변수를 포함해야 하고,
    
  • 변수들 간 다중공선성이 없어야 함.

CRM 가정

1. 기대값 독립성 (Mean Independence): 오차의 조건부 평균이 0이어야 함.
   \[ E[\varepsilon | x] = 0 \]
   이는 또한 \[ Cov(\varepsilon, x) = 0 \] 를 의미하며, 즉 오차항과 설명변수(들)가 상관이 없어야 함.

• 이 가정을 위반하면 \(\beta_k\)의 추정값이 편향됨.

오차 기대값 독립성: \(E[u | small] = ?\)

오차 기대값 독립성: \(E[u | small] = ?\)

외생성 (Exogeneity) 가정

• CRM 가정 #1은 (엄격한) 외생성 가정이라고도 불림.

• 이 가정이 위반되면, 추정량 \(b\)는 \(\beta\)의 편향된 추정값이 됨, 즉
  \[ \mathop{\mathbb{E}}[b] \neq \beta \]

• 예를 들어, 교육이 임금에 미치는 영향을 분석한다고 가정하자.

  \[ \text{wage}_i = \beta_0 + \beta_1 \text{education}_i + \varepsilon_i \]

  • 외생성 가정이 성립하면, \(\beta_1\)은 모집단에서 교육의 인과적 효과를 나타냄.

• 하지만 관찰되지 않은 능력 \(a_i\)가 존재한다고 가정하자.

  • 높은 능력을 가진 사람은 더 높은 임금을 받을 가능성이 큼.
  • 또한, 능력이 높으면 학교 생활이 더 쉬워지고, 따라서 더 많은 교육을 받게 될 가능성이 높음.

외생성 (Exogeneity) 가정

• 능력 \(a_i\)는 관찰되지 않기 때문에, 오차항 \(\varepsilon_i\)에 포함됨.

• 따라서, 기타 모든 조건이 동일하다는 가정 (ceteris paribus) 이 성립하지 않음.

• 그러면 임금을 교육 수준에 회귀 분석하면, 실제로는 능력 \(a_i\)가 원인이 된 임금 효과를 education의 효과로 잘못 귀속하게 됨.

• 누락된 변수 편향 (Omitted Variable Bias, OVB) 공식:

  \[ \text{OVB} = \text{다중 회귀에서 누락된 변수의 회귀 계수} \times \frac{Cov(x,z)}{Var(x)} \]

• 따라서, 다음을 얻음:

  \[ \mathbb{E}(b_1) = \beta_1 + OVB > \beta_1 \]

• 해석: 모집단에서 반복적으로 표본을 추출하고 매번 \(b_1\)을 계산하면, 교육이 임금에 미치는 효과를 체계적으로 과대평가하게 됨.

CRM 가정

1. 기대값 독립성 (Mean Independence): 오차의 조건부 평균이 0이어야 함.
   \[ E[\varepsilon | x] = 0 \]
   이는 또한 \[ Cov(\varepsilon, x) = 0 \] 를 의미하며, 즉 오차항과 설명변수(들)가 상관이 없어야 함.

• 이 가정을 위반하면 \(\beta_k\)의 추정값이 편향됨.

2. 독립적이고 동일한 분포 (Independently and Identically Distributed, i.i.d.): 데이터는 크기 \(n\)의 랜덤 표본에서 추출됨. 각 관측치 \((x_i, y_i)\)는 동일한 분포에서 나왔으며, 모든 \(i \neq j\)에 대해 \((x_j, y_j)\)와 독립적이어야 함.

   • 이 가정을 위반하면 표본이 모집단을 덜 대표하게 됨. 결과적으로 \(\beta_k\)의 추정값이 편향됨.

CRM 가정

3. 등분산성 (Homoskedasticity): 오차항 \(\varepsilon\)의 분산이 모든 \(x\) 값에 대해 동일해야 함. \[ Var(\varepsilon|x) = \sigma^2 \]

   • 이 가정이 위반되더라도 \(\beta_k\)의 추정값은 여전히 편향되지 않음. 그러나 \(\hat{\textrm{SE}}(b_k)\)의 추정값이 편향될 수 있으며, 이는 검정 통계량과 p-값에 영향을 미침.

4. 정규성 가정 (Normally Distributed Errors): 오차항이 정규 분포를 따라야 함. \(\varepsilon \sim \mathcal{N}(0, \sigma^2)\)

   • 엄격히 필수적인 것은 아니지만, 표본 크기가 작을 때도 추론이 가능하도록 도움을 줌.

👉 핵심 정리: 가정이 위반되면, 추론이 유효하지 않음!

Task 3-1

10:00

다시 교육과 성별이 임금에 미치는 효과에 대한 질문으로 돌아가 보겠음.

1. AER 패키지에서 CPS1985 데이터를 로드하고, 각 변수의 정의를 확인: ?CPS1985

2. wage의 로그 값을 log_wage 변수로 생성.

3. log_wage를 gender와 education에 회귀 분석하고, 결과를 reg1으로 저장.

• 각 계수를 해석하시오.
• 계수들이 통계적으로 유의한가? 어느 유의수준에서 유의한가?

4. log_wage를 gender, education 그리고 gender*education의 상호작용 항과 함께 회귀 분석하고, 결과를 reg2로 저장.

• \(female \times education\) 에 해당하는 계수를 어떻게 해석할 수 있는가?
• 이 계수의 귀무가설을 5% 유의수준에서 기각할 수 있는가? 10% 유의수준에서는?

Task 3-2

10:00

1. 로그 임금과 교육 수준 간의 관계를 나타내는 산점도를 생성하라.

2. geom_smooth를 사용하여 회귀선을 추가하라. 이 선이 무엇을 나타내는가?

3. 음영 영역이 무엇을 의미하는지 설명하라.

• cps 데이터에서 하나의 부트스트랩 표본을 추출하라.

• log_wage를 gender, education, 그리고 gender*education의 상호작용 항과 함께 회귀 분석하고, 결과를 reg_bootstrap으로 저장하라.

• reg_bootstrap에서 남성의 절편 값을 intercept_men_bootstrap으로, 기울기 값을 slope_men_bootstrap으로 추출하여 저장하라. 여성의 경우도 동일하게 수행하라.

• 이전 플롯에 이 부트스트랩 표본에서 예측된 두 회귀선을 추가하라 (힌트: geom_abline을 두 번 사용하라).

불확실성 시각화

이제 동일한 절차를 100번 반복해 보겠음!

library(AER)
data("CPS1985")
cps = CPS1985 %>% mutate(log_wage = log(wage))

set.seed(1)
bootstrap_sample = cps %>% 
    rep_sample_n(size = nrow(cps), reps = 100, replace = TRUE)

ggplot(data=cps,aes(y = log_wage, x = education, colour = gender)) +
  geom_point(size = 1, alpha = 0.7) +
  geom_smooth(method = "lm", alpha = 2) +
  geom_smooth(data=bootstrap_sample,
              size = 0.2,
              aes(y = log_wage, x = education, group = replicate),
              method = "lm", se = FALSE) +
  facet_wrap(~gender) +
  scale_colour_manual(values = c("darkblue", "darkred")) +
  labs(x = "Education", y = "Log wage") +
  guides(colour=FALSE) +
  theme_bw(base_size = 20)

불확실성 시각화

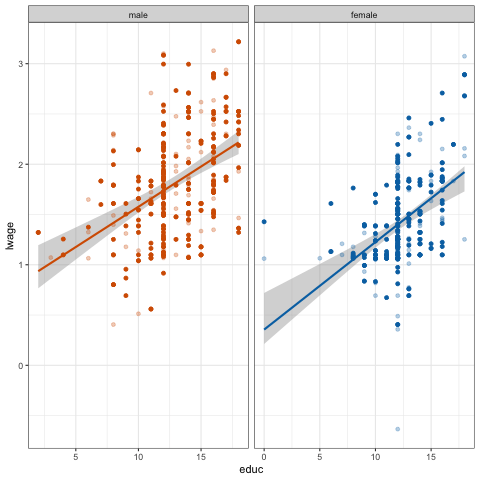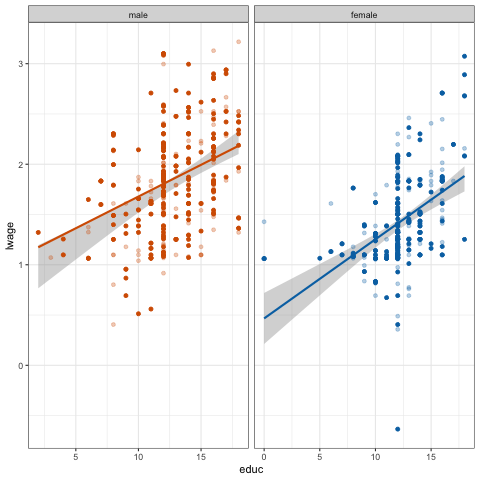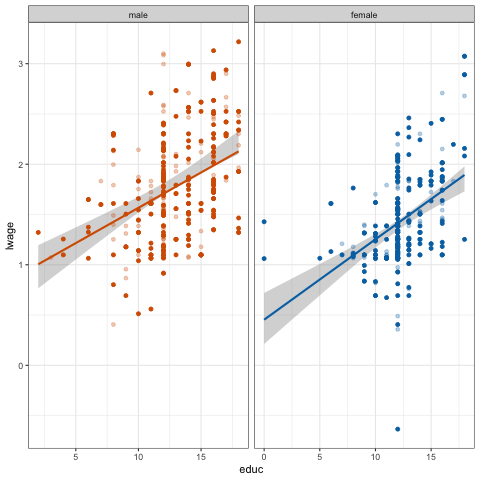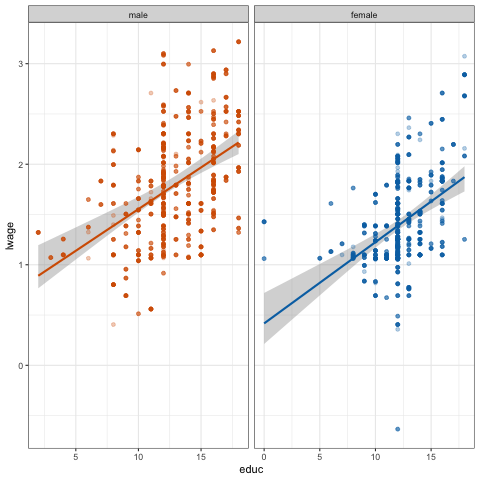
ungeviz와 gganimate를 사용하면 움직이는 선을 만들 수 있음!

• 데이터에서 20개의 부트스트랩 표본을 추출했음.
• 각 부트스트랩 표본에 포함된 데이터 포인트가 다름을 확인할 수 있음.
• 이러한 차이는 서로 다른 회귀선을 의미함.
• 평균적으로, 이 회귀선의 95%가 음영 영역 안에 포함되어야 함.
• 음영 영역을 볼 때, 이 움직이는 선을 기억해야 함!

🔍 인과 관계를 찾아가는 길

✅ 데이터를 어떻게 다룰까?: 읽기(Read), 정리(Tidy), 시각화(Visualize)…

✅ 변수간 관계를 어떻게 요약할까? 단순 / 다중 선형 회귀…비선형회귀, 교차변수…

✅ 인과 관계(Causality)란 무엇인가?

✅ 전체 모집단을 관측하지 못하면 어떻게 할까? Sampling!

✅ 우리의 연구 결과가 단순한 무작위(Randomness) 때문일 수도 있을까? 신뢰구간과 가설검정. 통계적 추론

❌ 실제로 외생성을 어떻게 찾아낼 수 있을까?

THE END!