FMB819: R을 이용한 데이터분석

Difference-in-Differences

Today’s Agenda

이중차분법 (Differences-in-Differences)

• 시간에 따른 정책 변화가 모든 사람에게 동일하게 영향을 미치지 않는 점을 활용함.
• 적절한 대조군(control group)을 찾아야 하거나 구성해야 함.
• 핵심 가정: 평행 추세 가정 (Parallel Trends Assumption)
• 실증적 적용: 최저임금이 고용에 미치는 영향 분석

Evaluation methods

• 다중 회귀 분석은 종종 관찰되지 않은 요인에 의한 선택(selection on unobservables) 때문에 인과적 추정치를 제공하지 못함.

• RCT(무작위 대조 실험)는 이러한 문제를 해결하는 한 가지 방법이지만, 현실적으로 시행이 불가능한 경우가 많음.

• 경제학에서 널리 사용되는 네 가지 주요 인과적 평가 방법:

  • 도구변수법 (Instrumental Variables, IV),
  • 성향 점수 매칭 (Propensity-Score Matching),
  • 이중차분법 (Differences-in-Differences, DiD), 및
  • 회귀 불연속 설계 (Regression Discontinuity Designs, RDD).

• 이러한 방법들은 처치(treatment)와 결과(outcome) 간의 __인과 관계__를 식별하는 데 사용됨.

• 이번 강의에서는 널리 사용되며 엄격한 프로그램 평가 방법인 __이중차분법(Differences-in-Differences)__을 다룰 것임.

Differences-in-Differences (DiD)

DiD의 요구사항

• 두 개의 시점: 처치 전과 처치 후.

• 두 개의 그룹:

  • 대조군(Control group): 처치를 전혀 받지 않는 집단.
  • 처치군(Treatment group): 초기에는 처치를 받지 않다가 이후 완전히 처치를 받는 집단.

• 특정 가정하에서, 대조군을 처치군의 반사실적(counterfactual) 비교 대상으로 사용할 수 있음.

예제: 최저임금과 고용

• 최저임금 인상이 (실업을 포함한) 고용에 미치는 인과적 영향을 평가하고자 한다고 가정하자.

• 하지만 이는 단순하지 않음. 적절한 대조군은 무엇이어야 할까?

• 노동경제학자 데이비드 카드(David Card)와 앨런 크루거(Alan Krueger)의 1994년 대표 논문 (링크)

  • 논문 제목: “최저임금과 고용: 뉴저지와 펜실베이니아 패스트푸드 산업 사례 연구”

• 이 연구는 최저임금 인상이 패스트푸드 산업의 고용률에 미치는 영향을 추정함. 왜 하필 이 산업을 선택했을까?

제도적 배경

• 미국에는 연방 최저임금이 있지만, 각 주는 이를 다르게 설정할 수 있음.

• 1992년 4월 1일: 뉴저지의 최저임금이 시간당 $4.25에서 $5.05로 인상됨.

• 반면, 인접한 펜실베이니아는 최저임금을 변경하지 않음.

펜실베이니아와 뉴저지는 매우 유사함: 제도, 생활습관, 소비자, 소득 수준, 기후 등 많은 면에서 비슷함.

Card and Krueger (1994): 방법론

• 뉴저지(NJ)와 동부 펜실베이니아의 패스트푸드점 410곳을 조사함.

• 조사 시점:

  • 뉴저지 최저임금 인상 전 조사: 1992년 2~3월
  • 뉴저지 최저임금 인상 후 조사: 1992년 11~12월

• 연구자들은 어떤 비교를 수행했을까?

좀 더 자세히 데이터를 살펴보자

# 패키지 설치 및 데이터 로드
remotes::install_github("b-rodrigues/diffindiff")
library(diffindiff)
ck1994 <- njmin

# A tibble: 6 × 6
  sheet chain  state        observation   empft emppt
  <chr> <chr>  <chr>        <chr>         <dbl> <dbl>
1 46    bk     Pennsylvania February 1992  30    15  
2 49    kfc    Pennsylvania February 1992   6.5   6.5
3 506   kfc    Pennsylvania February 1992   3     7  
4 56    wendys Pennsylvania February 1992  20    20  
5 61    wendys Pennsylvania February 1992   6    26  
6 62    wendys Pennsylvania February 1992   0    31  

Task 1

10:00

1. 데이터셋을 살펴보고 변수 목록을 확인하라. 변수 정의는 ?njmin을 사용하여 확인하라.

1. state 및 설문조사 시점(observation)별로 매장의 개수를 표로 정리하라. 해당 결과가 논문의 표 1과 일치하는지 확인하라.

2. 카드와 크루거(1994)의 방식에 따라, 정규직 상당(full-time equivalent, FTE) 고용 변수를 생성하라. empfte 변수를 정의하고 다음 식을 사용하라:

   empfte = empft + 0.5 * emppt + nmgrs

   여기서 empft는 정규직 직원 수, emppt는 시간제 직원 수, nmgrs는 매니저 수를 의미함.

3. state 및 설문조사 시점(observation)별로 다음 지표들의 평균을 계산하라.

   • FTE 고용 인원 수
   • 정규직 직원 비율(FTE 직원 대비 정규직 비율)
   • 평균 초봉(wage_st) 계산한 결과를 논문의 표 2와 비교하라.

4. 최저임금 인상 전, 뉴저지와 펜실베이니아의 패스트푸드점에는 어떤 차이가 있었는가?

Card and Krueger DiD: 결과

뉴저지 최저임금 인상 전후 평균 고용

Variables	Pennsylvania	New Jersey
FTE employment before	23.33	20.44
FTE employment after	21.17	21.03
Change in mean FTE employment	-2.17	0.59

DiD 추정치

• 이중차분(DiD) 인과 추정치: \(0.59 - (-2.17) = 2.76\)

• 해석: 최저임금 인상은 매장당 평균 FTE 고용 증가를 2.76명 초래함.

• 이중차분(DiD)의 핵심 개념은 이처럼 간단함! 😃

• 이제 이러한 결과를 그래픽으로 살펴보자.

DiD 그래프로 표현

DiD 그래프로 표현

DiD 그래프로 표현

DiD 그래프로 표현

DiD 그래프로 표현

DiD 그래프로 표현

만약 단순한 사후/사전 비교를 했다면 어떻게 되었을까?

만약 단순한 사후/사전 비교를 했다면 어떻게 되었을까?

만약 단순한 사후/사전 비교를 했다면 어떻게 되었을까?

만약 단순한 사후/사전 비교를 했다면 어떻게 되었을까?

Estimation

회귀 분석을 통한 DiD

• 실제 분석에서는, DiD는 보통 단 2개의 시점(4개의 관측치)보다 더 많은 기간을 포함하여 추정됨.

• 정책 변화 전후로 더 많은 데이터가 존재하는 경우가 많음.

DiD 회귀 분석의 3가지 핵심 요소

1. 처치 더미 변수 (Treatment Dummy Variable): \(TREAT_s\) (첨자 \(s\)는 처치가 주(state) 수준에서 이루어짐을 나타냄)

2. 정책 시행 이후 기간을 나타내는 더미 변수 (Post-Treatment Periods Dummy Variable): \(POST_t\) (첨자 \(t\)는 이 변수가 시간에 따라 변화함을 나타냄)

3. 두 변수의 상호작용항 (Interaction Term): \(TREAT_s \times POST_t\) 👉 이 항의 계수가 바로 DiD 인과 효과를 의미함!

회귀 분석을 통한 DiD

1. 처치 더미 변수 (Treatment Dummy Variable): \[ TREAT_s = \begin{cases} 0 \quad \text{if } s = \text{Pennsylvania} \\ 1 \quad \text{if } s = \text{New Jersey} \end{cases} \]

2. 정책 시행 이후 기간을 나타내는 더미 변수 (Post-Treatment Periods Dummy Variable): \[ POST_t = \begin{cases} 0 \quad \text{if } t < \text{April 1, 1992} \\ 1 \quad \text{if } t \geq \text{April 1, 1992} \end{cases} \]

3. 두 변수의 상호작용항 (Interaction Term): \(TREAT_s \times POST_t\) 👉 이 항의 계수가 바로 DiD 인과 효과를 의미함!

어떤 관측치에서 \(TREAT_s \times POST_t = 1\)이 되는가?

• 위 요소들을 모두 결합하면 다음과 같은 DiD 회귀식을 얻음: \[ EMP_{st} = \alpha + \beta TREAT_s + \gamma POST_t + \delta(TREAT_s \times POST_t) + \varepsilon_{st} \]

• \(\delta\): 최저임금 인상이 고용에 미치는 인과적 효과

회귀 분석 이해하기

\[EMP_{st} = \color{#d96502}\alpha + \color{#027D83}\beta TREAT_s + \color{#02AB0D}\gamma POST_t + \color{#d90502}\delta(TREAT_s \times POST_t) + \varepsilon_{st}\]

주어진 조건에서 기대값:

• \(\mathbb{E}(EMP_{st} \; | \; TREAT_s = 0, POST_t = 0) = \color{#d96502}\alpha\)

• \(\mathbb{E}(EMP_{st} \; | \; TREAT_s = 0, POST_t = 1) = \color{#d96502}\alpha + \color{#02AB0D}\gamma\)

• \(\mathbb{E}(EMP_{st} \; | \; TREAT_s = 1, POST_t = 0) = \color{#d96502}\alpha + \color{#027D83}\beta\)

• \(\mathbb{E}(EMP_{st} \; | \; TREAT_s = 1, POST_t = 1) = \color{#d96502}\alpha + \color{#027D83}\beta + \color{#02AB0D}\gamma + \color{#d90502}\delta\)

DiD 계산 과정

\[[\mathbb{E}(EMP_{st} \; | \; TREAT_s = 1, POST_t = 1)-\mathbb{E}(EMP_{st} \; | \; TREAT_s = 1, POST_t = 0)] - \\ [\mathbb{E}(EMP_{st} \; | \; TREAT_s = 0, POST_t = 1)-\mathbb{E}(EMP_{st} \; | \; TREAT_s = 0, POST_t = 0)] = \color{#d90502}\delta\]

회귀 분석 이해하기

\[EMP_{st} = \color{#d96502}\alpha + \color{#027D83}\beta TREAT_s + \color{#02AB0D}\gamma POST_t + \color{#d90502}\delta(TREAT_s \times POST_t) + \varepsilon_{st}\]

표 형식으로 정리:

	사전 평균	사후 평균	변화 (사후 - 사전)
펜실베이니아 (PA)	\(\color{#d96502}\alpha\)	\(\color{#d96502}\alpha + \color{#02AB0D}\gamma\)	\(\color{#02AB0D}\gamma\)
뉴저지 (NJ)	\(\color{#d96502}\alpha + \color{#027D83}\beta\)	\(\color{#d96502}\alpha + \color{#027D83}\beta + \color{#02AB0D}\gamma + \color{#d90502}\delta\)	\(\color{#02AB0D}\gamma + \color{#d90502}\delta\)
변화 (NJ - PA)	\(\color{#027D83}\beta\)	\(\color{#027D83}\beta + \color{#d90502}\delta\)	\(\color{#d90502}\delta\)

• 이 표는 펜실베이니아를 대조군(Control)으로, 뉴저지를 처치군(Treatment)으로 대체하여 일반적인 설정으로 확장할 수 있음.

Task 2

10:00

1. 더미 변수 treat를 생성하라. state가 펜실베이니아이면 FALSE, 뉴저지이면 TRUE로 설정하라.

2. 더미 변수 post를 생성하라. observation이 1992년 2월이면 FALSE, 그 외의 경우 TRUE로 설정하라.

3. 다음 회귀 모형을 추정하라. 슬라이드 9의 결과와 동일한 결과를 얻는가?

   \[empfte_{st} = \alpha + \beta treat_s + \gamma post_t + \delta(treat_s \times post_t) + \varepsilon_{st}\]

Identifying Assumptions

DiD의 핵심 가정: 평행 추세 (Parallel Trends)

공통 또는 평행 추세 가정: 최저임금이 인상되지 않았다면, 펜실베이니아의 패스트푸드 고용 추세는 뉴저지에서 기대할 수 있었던 추세와 같아야 함.

• 이 가정은 1992년 2월부터 11월까지 펜실베이니아의 패스트푸드 고용 추세가 뉴저지의 반사실적(counterfactual) 고용 추세를 신뢰할 수 있는 기준으로 제공해야 함을 의미함.

• 이 가정을 완전히 검증하거나 기각하는 것은 불가능함.

• 직관적인 확인 방법: 정책 변화 이전의 추세를 비교해보고, 중기적 효과가 없을 것으로 예상될 경우 정책 변화 이후의 추세도 비교해볼 수 있음.

평행 추세: 눈으로 확인

평행 추세 가정을 확인하는 방법

평행 추세 가정을 확인하는 방법

평행 추세 가정 ⟶ 검증됨 ✅

평행 추세 가정 ⟶ 검증됨 ✅

평행 추세 가정 ⟶ 검증되지 않음 ❌

평행 추세 가정 ⟶ 검증되지 않음 ❌

평행 추세 가정: Card and Krueger (2000)

펜실베이니아와 뉴저지의 실제 고용 추세를 살펴보자.

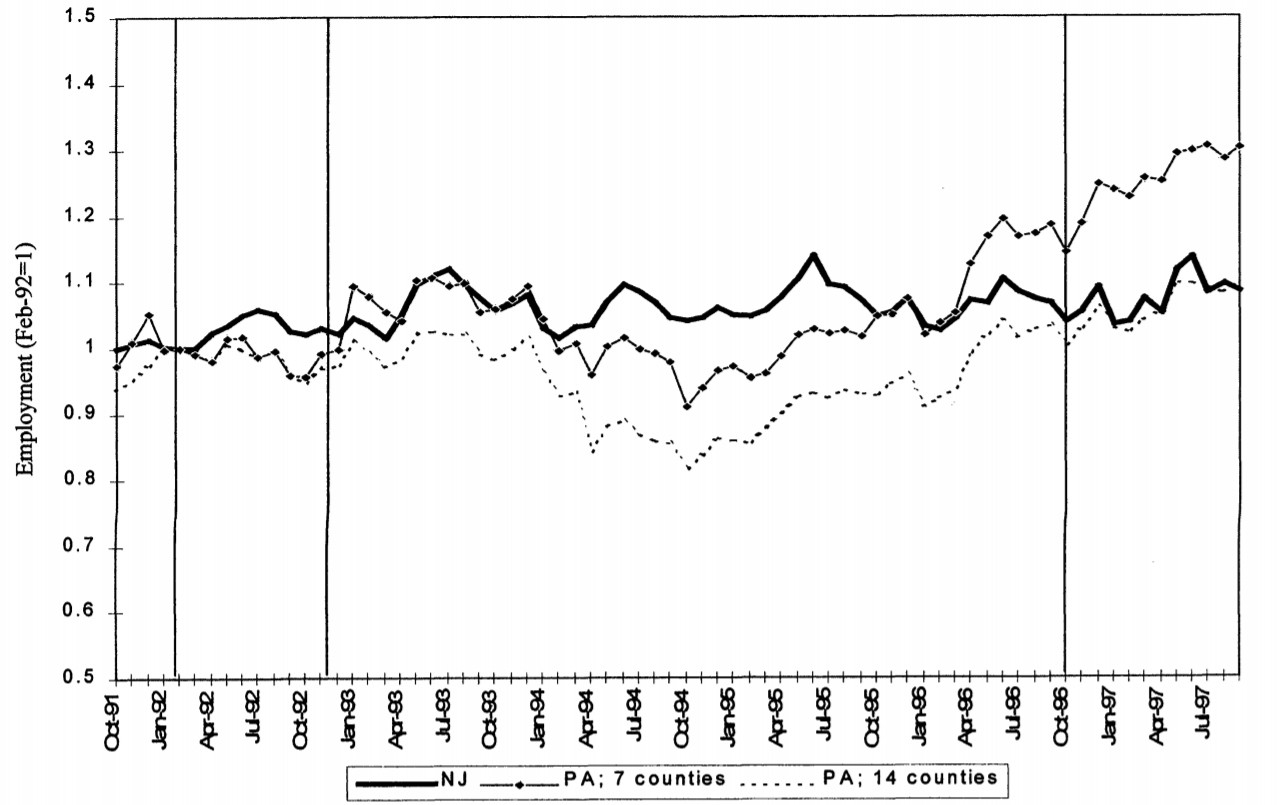
• 공통 추세 가정이 검증될 가능성이 높은가?

평행 추세 가정: 공식적 정의

다음과 같이 정의하자:

• \(Y_{ist}^1\): 시점 \(t\)에서 주(state) \(s\)의 식당 \(i\)에서 높은 최저임금이 적용될 경우 패스트푸드 고용 수준

• \(Y_{ist}^0\): 시점 \(t\)에서 주(state) \(s\)의 식당 \(i\)에서 낮은 최저임금이 적용될 경우 패스트푸드 고용 수준

이는 잠재적 결과(Potential Outcomes)이며, 두 개 중 하나만 관찰할 수 있음.

DiD 추정의 핵심 가정은, 처치(treatment)가 없을 경우 식당 \(i\)의 결과가 다음과 같이 주어진다는 것임:

\[\mathbb{E}[Y_{ist}^0|s,t] = \gamma_s + \lambda_t\]

이 가정은 두 가지 암묵적 가정을 포함함:

1. 선택 편향 (Selection Bias): 고정된 주(state) 특성 \((\gamma)\)과 관련됨.
2. 시간 추세 (Time Trend): 처치군과 대조군이 동일한 시간 추세 \((\lambda)\)를 가짐.

평행 추세 가정: 공식적 정의

비교 그룹에서의 결과:

\[\mathbb{E}[Y_{ist}| s = \text{Pennsylvania},t = \text{Feb}] = \gamma_{PA} + \lambda_{Feb}\]

\[\mathbb{E}[Y_{ist}|s = \text{Pennsylvania},t = \text{Nov}] = \gamma_{PA} + \lambda_{Nov}\]

\[ \begin{align} \mathbb{E}[Y_{ist}&|s = \text{Pennsylvania},t = \text{Nov}] - \mathbb{E}[Y_{ist}| s = \text{Pennsylvania},t = \text{Feb}] \\ &= \gamma_{PA} + \lambda_{Nov} - (\gamma_{PA} + \lambda_{Feb}) \\ &= \lambda_{Nov} - \lambda_{Feb} \end{align} \]

평행 추세 가정: 공식적 정의

비교 그룹에서의 결과:

\[\mathbb{E}[Y_{ist}| s = \text{Pennsylvania},t = \text{Feb}] = \gamma_{PA} + \lambda_{Feb}\]

\[\mathbb{E}[Y_{ist}|s = \text{Pennsylvania},t = \text{Nov}] = \gamma_{PA} + \lambda_{Nov}\]

\[ \begin{align} \mathbb{E}[Y_{ist}&|s = \text{Pennsylvania},t = \text{Nov}] - \mathbb{E}[Y_{ist}| s = \text{Pennsylvania},t = \text{Feb}] \\ &= \gamma_{PA} + \lambda_{Nov} - (\gamma_{PA} + \lambda_{Feb}) \\ &= \underbrace{\lambda_{Nov} - \lambda_{Feb}}_{\text{시간 추세 (time trend)}} \end{align} \]

\(\rightarrow\) 비교 그룹을 이용하여 시간 추세 (time trend)를 추정할 수 있음.

평행 추세 가정: 공식적 정의

비교 그룹에서의 결과:

\[\mathbb{E}[Y_{ist}| s = \text{Pennsylvania},t = \text{Feb}] = \gamma_{PA} + \lambda_{Feb}\]

\[\mathbb{E}[Y_{ist}|s = \text{Pennsylvania},t = \text{Nov}] = \gamma_{PA} + \lambda_{Nov}\]

\[ \begin{align} \mathbb{E}[Y_{ist}&|s = \text{Pennsylvania},t = \text{Nov}] - \mathbb{E}[Y_{ist}| s = \text{Pennsylvania},t = \text{Feb}] \\ &= \gamma_{PA} + \lambda_{Nov} - (\gamma_{PA} + \lambda_{Feb}) \\ &= \underbrace{\lambda_{Nov} - \lambda_{Feb}}_{\text{시간 추세 (time trend)}} \end{align} \]

\(\rightarrow\) 비교 그룹을 이용하여 시간 추세 (time trend)를 추정할 수 있음.

평행 추세 가정: 처치군의 결과

최저임금 인상의 진짜 효과(true impact)를 \(\delta\)라고 하자:

\[\mathbb{E}[Y_{ist}^1 - Y_{ist}^0|s,t] = \delta\]

처치군에서의 결과:

\[\mathbb{E}[Y_{ist}|s = \text{New Jersey}, t = \text{Feb}] = \gamma_{NJ} + \lambda_{Feb}\]

\[\mathbb{E}[Y_{ist}|s = \text{New Jersey}, t = \text{Nov}] = \gamma_{NJ} + \delta + \lambda_{Nov}\]

\[ \begin{align} \mathbb{E}[Y_{ist}&|s = \text{New Jersey}, t = \text{Nov}] - \mathbb{E}[Y_{ist}|s = \text{New Jersey}, t = \text{Feb}] \\ &= \gamma_{NJ} + \delta + \lambda_{Nov} - (\gamma_{NJ} + \lambda_{Feb}) \\ &= \delta + \underbrace{\lambda_{Nov} - \lambda_{Feb}}_{\text{시간 추세 (time trend)}} \end{align} \]

평행 추세 가정: 최종 도출

결과적으로:

\[ \begin{align} \mathbb{E}[Y_{ist}&|s = \text{PA},t = \text{Nov}] - \mathbb{E}[Y_{ist}| s = \text{PA},t = \text{Feb}] = \underbrace{\lambda_{Nov} - \lambda_{Feb}}_{\text{시간 추세 (time trend)}} \end{align} \]

\[ \begin{align} \mathbb{E}[Y_{ist}&|s = \text{NJ},t = \text{Nov}] - \mathbb{E}[Y_{ist}| s = \text{NJ},t = \text{Feb}] = \delta + \underbrace{\lambda_{Nov} - \lambda_{Feb}}_{\text{시간 추세 (time trend)}} \end{align} \]

\[ \begin{align} DD &= \mathbb{E}[Y_{ist}|s = \text{NJ}, t = \text{Nov}] - \mathbb{E}[Y_{ist}|s = \text{NJ}, t = \text{Feb}] \\ & \qquad \qquad - \Big(\mathbb{E}[Y_{ist}|s = \text{PA},t = \text{Nov}] - \mathbb{E}[Y_{ist}| s = \text{PA},t = \text{Feb}]\Big) \\ &= \delta + \lambda_{Nov} - \lambda_{Feb} - (\lambda_{Nov} - \lambda_{Feb}) \\ &= \delta \end{align} \]

🔍 인과 관계를 찾아가는 길

✅ 데이터를 어떻게 다룰까?: 읽기(Read), 정리(Tidy), 시각화(Visualize)…

✅ 변수간 관계를 어떻게 요약할까? 단순 / 다중 선형 회귀…비선형회귀, 교차변수…

✅ 인과 관계(Causality)란 무엇인가?

✅ 전체 모집단을 관측하지 못하면 어떻게 할까? Sampling!

✅ 우리의 연구 결과가 단순한 무작위(Randomness) 때문일 수도 있을까? 신뢰구간과 가설검정. 통계적 추론

🚧 실제로 외생성을 어떻게 찾아낼 수 있을까?: 이중 차분

THE END!