Introduction to Causality

FMB819: R을 이용한 데이터분석

고려대학교 경영대학 정지웅

Today’s Agenda

  • 인과관계(Causality) vs. 상관관계(Correlation)

  • 잠재 결과 프레임워크(Potential Outcomes Framework)

  • 무작위 통제 실험(Randomized Controlled Trials, RCTs)

  • 학급 규모(class size)와 학생 성취(student performance)에 대한 실증 분석 심화

상관관계 vs. 인과관계

  • “상관관계는 인과관계가 아니다”라는 말은 매우 흔하게 사용됨.
    그런데 왜 이것이 사실인지 설명할 수 있는가?

  • 일부 상관관계는 명백히 인과관계를 의미하지 않음.
    (예: 가짜 상관관계 모음 링크)

상관관계 vs. 인과관계: 흡연과 폐암

  • 상관관계와 인과관계를 구분하기 어려운 경우가 잦음.

  • 흡연이 폐암을 유발하는가?

  • 오늘날 우리는 답이 “예(YES)”라는 것을 알고 있음!

  • 하지만 1950년대에는…

    • 당시 폐암 사망률이 급격히 증가하기 시작함…
    • … 그리고 그 이전에 담배 소비가 빠르게 증가했음.

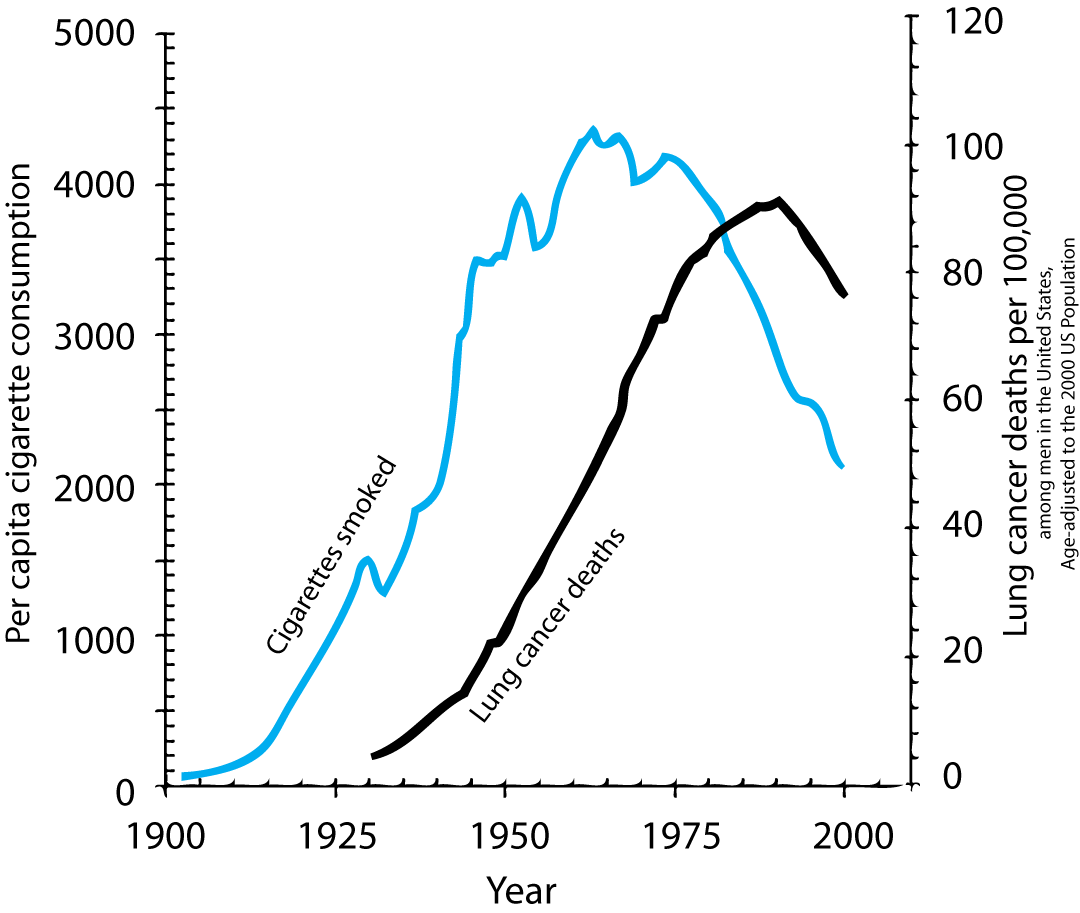
  • 이 그래프만 보면, “흡연이 폐암을 유발한다”고 쉽게 결론 내릴 수 있음.

상관관계 vs. 인과관계: 흡연과 폐암

  • 하지만 당시 회의적인 사람들이 많았으며, 유명한 통계학자들조차도 이 관계를 의심했음.

거시적 교란 요인 (Macro Confounding Factors)

  • 폐암을 유발할 수 있는 다른 거시적 요인들도 1900년~1950년 사이에 변화했음:

    • 도로 포장(tarring of roads),
    • 자동차 배기가스(납 함유 가솔린 연기) 흡입,
    • 전반적인 대기 오염 증가.

자기 선택 편향 (Self Selection)

  • 흡연자와 비흡연자는 원래부터 다를 가능성이 있음:

    • 관측 가능한 특징에 따른 선택(selection on observables): 연령, 교육 수준, 소득 등.

    • 관측 불가능한 특징에 따른 선택(selection on unobservables): 유전자?

상관관계 vs. 인과관계: 다른 예시들

  • 교육 연수(years of education) \(\rightarrow\) 소득?

    • 개인이 교육 수준을 선택하는 방식이 다를 수 있음. 고등 교육을 받는 사람들은 원래부터 높은 선천적 능력을 가졌거나, 학교 생활을 즐기며 학업에 강한 성향을 가질 가능성이 높음. \(\rightarrow\) 자기 선택 편향(Self-selection)

  • 최저임금 \(\rightarrow\) 고용률(employment rate)? - 정책 결정자들은 고용률이 높은 시기에 최저임금을 인상할 가능성이 있음. \(\rightarrow\) 역인과관계(reverse causality) / 동시성(simultaneity)

  • 금융 발전 \(\rightarrow\) 경제 성장?

    • 경제 성장이 금융 발전을 촉진하는 것일 수도 있음 (반대로 금융 발전이 경제 성장을 유발하는 것이 아닐 가능성) \(\rightarrow\) 역인과관계(reverse causality) / 동시성(simultaneity)

내생성 (Endogeneity)

  • 개인은 자신의 효용(utility)을 극대화(maximise)하기 위해 행동한다면…

  • 개인들은 무작위(random ways)로 행동하지 않음. \(\rightarrow\) 즉, 개인의 행동은 내생적(endogenous)이라고 볼 수 있음.

  • 데이터에서 발견된 상관관계를 무조건 믿어서는 안 됨. 언제나 의심하는 태도가 필요함.

  • 📌 그렇다면, 어떻게 인과적 주장(causal claims)을 할 수 있을까?

  • 잠재 결과 프레임워크(Potential Outcomes Framework)가 유용한 길잡이.

인과관계의 개념

인과관계(Causality)란 무엇을 의미하는가?

  • X가 Y를 유발한다(causes)… 의미?

  • 만약 다른 모든 것은 그대로 둔 채 우리가 X의 값을 변경(intervene and change)한다면,

  • 그 결과로 Y도 변화하게 된다는 의미.

  • 여기서 핵심은 “다른 모든 것은 그대로 둔다”는 가정임.
    이는 흔히 “세테리스 파리부스(ceteris paribus, all else equal)” 가정이라고 불림.

  • 하지만, 이것은 X가 Y를 유발하는 유일한 요인이라는 뜻이 아님!

Causal Inference

The Potential Outcomes Framework

이 모델은 Rubin의 인과 모델(Rubin Causal Model)이라고도 불리며, 통계학자 Donald Rubin이 1970년대에 이를 일반화하고 체계화함.

  • 핵심 아이디어 (Key Idea)

    • 각 개인은 여러 개의 대체적 처치 상태(alternative treatment states)에 노출될 수 있음.

      • 담배를 피우거나, 시가를 피우거나, 아예 피우지 않거나.
      • 소규모 학급과 대규모 학급에서 배우는 것.

  • 처치 변수 \(D_i\)를 이진 변수(binary variable)로 정의 $$

\[ D_i = \begin{cases} 1 \textrm{ if individual $i$ is treated} \\\\ 0 \textrm{ if individual $i$ is not treated} \end{cases} \]

✅ Treatment group
all the individuals such that \(D_i = 1\).

❌ Control group
all the individuals such that \(D_i = 0\).

The Potential Outcomes Framework

  • 이 프레임워크에서는 각 개인이 두 개의 잠재적 결과(potential outcomes)를 가짐. 하지만 실제로는 하나의 관측된 결과(observed outcome) \(Y_i\)만 확인 가능함.

    • \(Y_i^1\): 개인 \(i\)가 처치를 받았을 경우의 잠재적 결과 \((D_i = 1)\)
    • \(Y_i^0\): 개인 \(i\)가 처치를 받지 않았을 경우의 잠재적 결과 \((D_i = 0)\)

  • 현실에서는 단 하나의 결과 \(Y_i\)만을 관측할 수 있으며, 이는 다음과 같이 표현됨: \[ Y_i = D_i \times Y_i^1 + (1- D_i) \times Y_i^0 \]

  • 🔥 인과 추론의 근본적인 문제 (Fundamental Problem of Causal Inference) 어떤 개인 \(i\)에 대해, 두 개의 잠재적 결과 중 오직 하나만 관측할 수 있음. (Holland, 1986).

The Potential Outcomes Framework

  • 관측되지 않은 잠재적 결과도 이론적으로 존재한다고 보며, 이를 반사실적 결과(counterfactual outcome)라고 함.
Group \(Y_i^1\) \(Y_i^0\)
처치 그룹 \((D_i = 1)\) ✅ 관측 가능 (Observed as \(Y_i\)) ❌ 반사실적 결과 (Counterfactual)
통제 그룹 \((D_i = 0)\) ❌ 반사실적 결과 (Counterfactual) ✅ 관측 가능 (Observed as \(Y_i\))

  • 위 개념을 바탕으로, 개별 처치 효과(individual treatment effect) \(\delta_i\)를 정의할 수 있음. \[ \delta_i = Y_i^1 - Y_i^0 \]

  • \(\delta_i\)는 처치 \((D_i)\)가 개인 \(i\)의 결과 변수 \(Y\)에 미치는 인과적 효과(causal effect)를 측정함.

  • ⚠️ 핵심 문제: 개별 처치 효과 \(\delta_i\)는 개인 수준에서는 절대 관측할 수 없음! 대안: 집단 평균(population averages)을 이용.

보충 설명: 기대값 (Expectation)

  • 🎲 주사위를 무한히 던지면 평균적으로 몇이 나올까?

    • \(X\)가 나온 숫자를 나타내는 확률 변수(random variable)라 하면, 기대값(expectation)은:

\[ \mathop{\mathbb{E}}(X) = \frac{1}{6} \times 1 + \frac{1}{6} \times 2 + \frac{1}{6} \times 3 + \frac{1}{6} \times 4 + \frac{1}{6} \times 5 + \frac{1}{6} \times 6 = 3.5 \]

  • \(\mathop{\mathbb{E}}(\cdot)\) 연산자는 기대값(expectation) 또는 모집단 평균(population mean)을 의미함.

  • \(\mathop{\mathbb{E}}(\cdot)\) 연산자는 선형(linear) 연산자이므로,

\[ \mathop{\mathbb{E}}(X+Y) = \mathop{\mathbb{E}}(X) + \mathop{\mathbb{E}}(Y) \] - 여기서 \(X\)와 \(Y\)는 두 개의 확률 변수임.

보충 설명: 조건부 기대값

  • 🎲 두 개의 주사위를 던질 때, 한 주사위가 5일 경우, 합의 평균은?

  • \(X\)가 첫 번째 주사위의 숫자를 나타내는 확률 변수, \(Y\)가 두 번째 주사위의 숫자를 나타내는 확률 변수라 하면:

\[ \begin{align} \mathop{\mathbb{E}}(X+Y|Y = 5) &= \mathop{\mathbb{E}}(X|Y = 5) + \mathop{\mathbb{E}}(Y|Y = 5) \\ &= \mathop{\mathbb{E}}(X) + 5 \\ &= 3.5 + 5 \\ &= 8.5 \end{align} \]

  • \(\mathop{\mathbb{E}}(\cdot|D = x)\) 연산자는 조건부 기대값(conditional expectation)을 의미함. 이는 모집단 전체가 아니라, 특정 조건(\(D = x\))을 만족하는 하위 집단(subcategory)에 대한 기대값을 계산하는 것.

평균 처치 효과 (Average Treatment Effect, ATE)

  • 가장 포괄적인 평균 효과

\[ \begin{align} ATE &= \mathop{\mathbb{E}}(\delta_i) \\ &= \mathop{\mathbb{E}}(Y_i^1 - Y_i^0) \\ &= \mathop{\mathbb{E}}(Y_i^1) - \mathop{\mathbb{E}}(Y_i^0) \end{align} \]

  • ATE는 단순히 전체 모집단에서 개별 처치 효과(individual treatment effects)의 평균을 측정하는 것.

🔗 부록(Appendix): 처치군에 대한 평균 처치 효과(ATT)와 비처치군에 대한 평균 처치 효과(ATU)

예제: 소규모 vs. 대규모 학급

  • 학생이 소규모 학급(\(Y^1\)) 또는 대규모 학급(\(Y^0\))에서 수업을 들을 경우, 평균 평점(GPA, 0-10)의 잠재적 결과(potential outcomes).

📊 잠재적 결과 테이블

학생 \(Y^1\) \(Y^0\) \(\delta\)
1 5 2 3
2 6 4 2
3 3 6 -3
4 5 4 1
5 10 8 2
6 2 4 -2
7 5 2 3
8 6 4 2
9 2 9 -7
10 8 2 6
평균 5.2 4.5 0.7

평균 처치 효과 (ATE) 계산

\[ \begin{align} \color{#d90502}{\text{ATE}} &= \mathbb{E}(\delta) \\ &=\mathbb{E}(Y^1) - \mathbb{E}(Y^0) \\ &= 5.2 - 4.5 \\ &= 0.7 \end{align} \]

\(\rightarrow\) 소규모 학급이 대규모 학급보다 평균적으로 GPA를 0.7점 높이는 효과가 있음.

  • ⚠️ 하지만 모든 학생이 동일한 처치 효과를 경험한 것은 아님!

인과 추론의 문제 (The Problem of Causal Inference)

  • 실제로 ATE를 계산할 때, 결측 데이터 문제(missing data problem)가 발생함.
    \(\delta_i\)를 계산할 때와 마찬가지로, 각 개인에 대해 \(Y_i^1\) 또는 \(Y_i^0\) 중 하나가 항상 누락됨.

-📊 데이터를 이용하면, 처치군과 통제군의 단순 평균 차(Simple Difference in mean Outcomes, SDO)가 계산됨.

\[ \begin{align} SDO &= \mathop{\mathbb{E}}(Y_i^1|D_i=1) - \mathop{\mathbb{E}}(Y_i^0|D_i=0) \\ &= \underbrace{\frac{1}{N_T}\sum_{i=1}^{N_T}(Y_i|D_i=1)}_{\text{처치군의 평균 결과}} - \underbrace{\frac{1}{N_C}\sum_{i=1}^{N_C}(Y_i|D_i=0)}_{\text{통제군의 평균 결과}} \end{align} \]

단순 평균 차이 (SDO): 예제

  • 🎓 학교장이 학생을 최적의 처치 그룹에 배정한다고 가정하자.
학생 \(Y^1\) \(Y^0\) \(\delta\) \(Y\) \(D\)
1 5 2 3
2 6 4 2
3 3 6 -3
4 5 4 1
5 10 8 2
6 2 4 -2
7 5 2 3
8 6 4 2
9 2 9 -7
10 8 2 6
평균 0.7

단순 평균 차이 (SDO): 예제

  • 🎓 학교장이 학생을 최적의 처치 그룹에 배정한다고 가정하자.
학생 \(Y^1\) \(Y^0\) \(\delta\) \(Y\) \(D\)
1 5 2 3 5 1
2 6 4 2 6 1
3 3 6 -3 6 0
4 5 4 1 5 1
5 10 8 2 10 1
6 2 4 -2 4 0
7 5 2 3 5 1
8 6 4 2 6 1
9 2 9 -7 9 0
10 8 2 6 8 1
평균 0.7

단순 평균 차이 (SDO): 계산

학생 \(Y\) (관측값) \(D\) \(\delta\)
1 5 1 3
2 6 1 2
3 6 0 -3
4 5 1 1
5 10 1 2
6 4 0 -2
7 5 1 3
8 6 1 2
9 9 0 -7
10 8 1 6
평균 0.7

🔢 단순 평균 차이 (SDO) 계산

\[ \begin{align} SDO &= \frac{5+6+5+10+5+6+8}{7} - \frac{6+4+9}{3} \\ &\approx 6.43 - 6.33 \approx 0.1 \end{align} \]

📌 SDO 값이 ATE(0.7)보다 작음!

📌 이러한 차이는 인과관계를 제대로 반영하지 못할 가능성이 높음.

📌 이런 “단순 비교”를 하면 안됨.

단순 비교의 문제점

📌 단순 평균 차이 (SDO)를 다시 작성하여 개별 처치 효과 \((\delta_i)\)가 나타나도록 변형 \[ \begin{align} SDO &= \mathop{\mathbb{E}}(Y_i^1|D_i=1) - \mathop{\mathbb{E}}(Y_i^0|D_i=0) \\ &= \mathop{\mathbb{E}}(Y_i^0 + \delta_i | D_i = 1) - \mathop{\mathbb{E}}(Y_i^0 | D_i = 0) \end{align} \]

✨ 가정: 모든 개인에 대해 처치 효과가 일정하다고 가정 하자. (즉, \(\delta_i = \delta\)) \[ SDO = \delta + \mathop{\mathbb{E}}(Y_i^0 | D_i = 1) - \mathop{\mathbb{E}}(Y_i^0 | D_i = 0) \]

그리고, \[ ATE = \mathop{\mathbb{E}}(\delta_i) = \mathop{\mathbb{E}}(\delta) = \delta \]

(위 가정에 의해) 따라서: \[ \begin{equation} SDO = ATE + \underbrace{\mathop{\mathbb{E}}(Y_i^0 | D_i = 1) - \mathop{\mathbb{E}}(Y_i^0 | D_i = 0)}_\text{선택 편향 (Selection Bias)} \end{equation} \]

🔗 부록(Appendix): 만약 처치 효과가 일정하다는 가정이 완화되면, 추가적인 편향 항(bias term)이 나타남.

Task 1

10:00

📂 1. 데이터 불러오기 및 변수 생성

  • 데이터 다운로드 링크. read.csv()를 사용하여 데이터를 불러오기.

  • 변수 설명

    • group_dummy: 처치를 받았는지 여부 (1 = 처치군, 0 = 통제군).
    • Y0: 처치를 받지 않았을 경우의 잠재적 결과 \((Y_i^0)\).
    • Y1: 처치를 받았을 경우의 잠재적 결과 \((Y_i^1)\).

  • 다음 변수들을 생성하시오.

    • 관측된 결과 \(Y_i = D_i \times Y_i^1 + (1 - D_i) \times Y_i^0\)
    • 개별 처치 효과 \(\delta_i = Y_i^1 - Y_i^0\)

📊 2. ATE 및 SDO 계산

  • ATE (Average Treatment Effect) 계산하시오.
  • SDO (Simple Difference in Mean Outcomes) 계산하시오.
  • Bias가 존재하는가? 크기는 얼마나 큰가?

🔀 3. 무작위 배정된 데이터에서 SDO 계산

  • 새로운 데이터 다운로드 링크. 이 데이터에서는 동일한 개인을 임의로 무작위 배정(random assignment)하였음.

  • \(Y_i\) 재계산 하시오. 새로운 처치 배정에 맞춰 다시 계산해야 함.

  • 무작위 배정에서 SDO 계산

    • 편향이 0에 가까운가?
    • 하지만 정확히 0이 되지 않는 이유는 무엇일까?

📌 4. (Optional) 편향 요소 확인

  1. 선택 편향(Selection Bias) 계산하시오.
  2. 이질적 처치 효과 편향(Heterogeneous Treatment Effect Bias) 계산하시오.
  3. 아래 식이 성립하는지 확인: \[ SDO = ATE + \text{Selection Bias} + \text{Heterogeneous Treatment Effect Bias} \]

무작위 배정(Randomization)을 통한 인과 추론 문제 해결

📌 무작위 실험(Randomized experiments):
- 사람들을 무작위(randomly)로 처치군과 통제군에 배정함.
- 이 경우, 처치 배정은 잠재적 결과(potential outcomes)와 독립적(independent).   - 즉 \(\mathbb{E}(Y_i^0 | D_i = 1)\)과 \(\mathbb{E}(Y_i^0 | D_i = 0)\)이 서로 다를 이유가 없음.
- 따라서, 선택 편향(selection bias)이 0이 됨.

✅ 무작위 배정이 이루어진다면:

\[ SDO = \mathop{\mathbb{E}}(Y_i^1|D_i=1) - \mathop{\mathbb{E}}(Y_i^0|D_i=0) = ATE \]

👉 즉, 데이터를 이용해 직접 ATE를 추정할 수 있음!

Randomized Experiments

무작위 실험 (Randomized Experiments)

  • 흔히 무작위 통제 실험(Randomized Controlled Trials, RCTs)이라고 불림.

  • 최초의 RCT는 18~19세기에 주로 의학 분야에서 수행됨.

  • 20세기 초반, 통계학자 J. Neyman과 R.A. Fisher에 의해 널리 보급됨.

  • 이후 공공정책 평가(public policy evaluation)의 신뢰할 수 있는 도구로 점차 자리 잡음.

  • 경제학(Economics)에서도 RCT의 영향력 증가

학급 규모와 학생 성취: 예제

지난 주, 학생들의 평균 수학 또는 읽기 점수(math/reading score)를 학급 규모(class size)에 대해 회귀 분석하였음.

\[ \textrm{math score}_i = b_0 + b_1 \textrm{class size}_i + e_i \]

그러나 \(b_1^{OLS}\)는 인과관계(causal relationship)가 아니라 단순한 상관관계(association)만을 보여줌.

📌 왜 OLS 계수 \(b_1\)이 인과관계를 추정할 수 없는가?

  1. 학생의 자기 선택(Student sorting): 학부모들이 작은 학급이 더 낫다는 선입견을 가지고 있다면, 자녀를 그런 학교에 보내려고 할 것.

  2. 교사의 자기 선택(Teacher sorting): 작은 학급이 가르치기 더 쉬움 → 교사들은 작은 학급이 있는 학교로 이동하려 할 것. 만약 작은 학급이 있는 학교에 경쟁이 존재한다면, 우수한 교사(high-quality teachers)가 더 유리할 가능성이 큼.

  3. 지역(Location effect): 대규모 학급은 부유한 대도시에서 더 흔할 수 있음. 소규모 학급은 가난한 농촌 지역에서 더 흔할 가능성이 있음.

✅ RCT를 수행하면 이러한 모든 편향(bias)을 제거할 가눙성이 높아짐

프로젝트 STAR 실험 (The Project STAR Experiment)

테네시 학생-교사 성취 비율 실험 (Tennessee Student/Teacher Achievement Ratio Experiment) 📖 Krueger (1999) 참고.

  • 테네시 주의회(Tennessee legislature)에서 총 약 1,200만 달러($12 million) 예산 지원. 1985-1986 학년도에 시작, 총 4년간 진행됨.

🔬 실험 설계

  • 11,600명의 학생과 교사가 무작위로(randomly assigned) 아래 3개 그룹 중 하나에 배정됨. 실험은 유치원부터 3학년까지(Kindergarten ~ 3rd grade) 지속됨.

    1️⃣ 소규모 학급: 학생 수: 13~17명 / 교사 1인

    2️⃣ 일반 학급 :학생 수: 22~25명 / 교사 1인

    3️⃣ 일반 학급 + 보조 교사: 학생 수: 22~25명 / 교사 1인 + 풀타임 보조 교사

📊 실험 과정

  • 각 학교 내에서 무작위 배정(randomization within schools) 진행.
  • 매년 3월경 학생들의 수학(Math) 및 읽기(Reading) 능력 평가 실시.

⚠️ 비랜덤 탈락 문제(Non-random Attrition)

  • 일부 학생들이 무작위 배정 이후 실험에서 이탈하는 문제 발생.
  • 그러나 여기에서는 해당 문제를 무시함.

Task 2

10:00

  1. 데이터 불러오기: 데이터 다운로드 링크
  • 데이터를 star_df 객체에 저장. 변수 설명 도움말 확인.
    (📌데이터가 재구성(reshaped)되어, 변수명 끝의 “k”, “1” 등의 숫자는 무시.)
  1. 데이터의 기본 정보 확인
  • 관찰 단위(Unit of observation)는 무엇인가?
    1. 랜덤 학급 배정(random class assignment): star, (ii) 학생의 학년(class grade): grade, (iii) 결과 변수(outcomes of interest): read & math
  1. 데이터 크기 및 결측값(NA) 분석
  • 총 관측치 수는 몇 개인가? 원래는 학생별로 관측단위였는데, 학년-학생 단위로 데이터를 재구조화하였기 때문에 NA 값이 많음. 또한 NA는 여러 가지 이유로 실험을 떠나게 된 학생들임.
  1. 결측값 처리 (NA 제거)
  • 다음 코드 실행하여 결측값이 없는 경우만 유지:
star_df <- star_df[complete.cases(star_df),] # 또는 star_df <- na.omit(star_df)
  1. 무작위 배정 확인 (Balancing Checks)
  • 랜덤 배정이 잘 이루어졌는지 확인하기 위해, 그룹별 기초 통계량을 계산.
  • 다음 항목별 평균 비율(%)을 학년별(grade) 및 처치군별(treatment class)로 비교: 1️⃣ 여학생 비율 (percentage of girls), 2️⃣ 아프리카계 미국인 비율 (percentage of African Americans), 3️⃣ 무료 급식 대상 비율 (percentage of free lunch qualifiers)을 살펴보자.

(📌 힌트: 다음 코드로 여학생 비율 계산 가능 (dplyr 활용 필요): share_female = mean(gender == "female") * 100.)

프로젝트 STAR 실험

✅ RCT에서 평균 처치 효과(ATE) 추정 방법

  • 무작위 통제 실험(RCT)에서는 처치군(treatment group)과 통제군(control group)의 결과 차이를 이용해 평균 처치 효과(ATE)를 추정할 수 있음.

다음과 같은 설정:

  • 처치군(Treatment Group): 소규모 학급(Small class)
  • 통제군(Control Group): 일반 학급(Regular class)
  • 대상 학년(Grade): 유치원(Kindergarten, k)
grade test mean regular mean small ATE
k math 484.45 493.34 8.9
k read 435.76 441.13 5.37

📌 이 ATE 값들의 해석은?

📉 회귀분석(regression)으로 표현할 수 있을까?

RCT를 회귀 분석 형태로 표현하기

🎯 RCT에서 결과 변수의 기본 표현

\[ Y_i = D_i Y_i^1 + (1 - D_i) Y_i^0 \]

✨ \(D_i\)로 묶어주고, \(Y_i^1 - Y_i^0\)를 \(\delta_i\)로 대체하면:

\[ \begin{align} Y_i &= Y_i^0 + D_i (Y_i^1 - Y_i^0) \\ &= Y_i^0 + D_i \delta_i \end{align} \]

📌 \(\delta_i = \delta\) (모든 \(i\)에 대해 동일한 처치 효과 가정)

\[ Y_i = Y_i^0 + D_i \delta \]

🔄 우항에 \(\mathbb{E}[Y_i^0] - \mathbb{E}[Y_i^0] = 0\)을 추가하면:

\[ \begin{align} Y_i &= \mathbb{E}[Y_i^0] + D_i \delta + Y_i^0 - \mathbb{E}[Y_i^0] \\ &= b_0 + \delta D_i + e_i \end{align} \]

여기서,
- \(b_0 = \mathbb{E}[Y_i^0]\) (통제군의 평균 결과)
- \(e_i = Y_i^0 - \mathbb{E}[Y_i^0]\) (오차항, 개별적 변동)

✅ 즉, RCT를 단순한 회귀 분석 형태로 나타낼 수 있음!
이제 실제 데이터에서 이를 어떻게 추정할지 살펴보자. 🚀

프로젝트 STAR 실험: 회귀 분석

✅ 소규모 학급에 배정된 것이 수학 성적에 미치는 ATE를 추정해보자.

📊 추정할 회귀 모델: \(\text{math score}_i = b_0 + \delta \text{small}_i + e_i\)

여기서,
\[ \text{small}_i = \begin{cases} 1 \quad \text{(소규모 학급 배정)} \\\\ 0 \quad \text{(일반 학급 배정)} \end{cases} \]

star_df_k_small <- star_df %>%
    filter(star %in% c("regular", "small") &
           grade == "k") %>% 
    mutate(small = (star == "small"))

star_df_k_small %>% count(star, grade)
## # A tibble: 2 × 3
##   star    grade     n
##   <chr>   <chr> <int>
## 1 regular k      1781
## 2 small   k      1578

프로젝트 STAR 실험: 회귀 분석

📌 추정할 회귀 모델 \(\text{math score}_i = b_0 + \delta \text{small}_i + e_i\)

## 
## Call:
## lm(formula = math ~ small, data = star_df_k_small)
## 
## Coefficients:
## (Intercept)    smallTRUE  
##     484.446        8.895

📌 회귀 분석 계수 의미 정리: \(b_0 = \mathbb{E}[Y_i^0]\) and \(\delta = \mathbb{E}[Y_i | D_i = 1] - \mathbb{E}[Y_i | D_i = 0]\)

  • \(b_0\): 통제군(일반 학급)의 평균 수학 점수
  • \(\delta\): 소규모 학급과 일반 학급의 평균 점수 차이
b_0 = mean(star_df_k_small$math[star_df_k_small$small == FALSE])
b_0
## [1] 484.4464
delta = mean(star_df_k_small$math[star_df_k_small$small == TRUE]) - mean(star_df_k_small$math[star_df_k_small$small == FALSE])
delta
## [1] 8.895193

더미 변수를 사용한 회귀 분석: 그래프

📌 회귀 분석의 독립 변수(regressor)는 더미 변수(dummy variable)

더미 변수를 사용한 회귀 분석: 그래프

📌 회귀 분석의 독립 변수(regressor)는 더미 변수(dummy variable)

더미 변수를 사용한 회귀 분석: 그래프

📌 회귀 분석의 독립 변수(regressor)는 더미 변수(dummy variable)

더미 변수를 사용한 회귀 분석: 그래프

📌 회귀 분석의 독립 변수(regressor)는 더미 변수(dummy variable)

더미 변수를 사용한 회귀 분석: 공식으로 표현

📌 회귀 모델: \(\text{math score}_i = b_0 + \delta \text{small}_i + e_i\)

📌 일반 학급(통제군, \(small_i = 0\))에서의 기대값 \[ \begin{align} \mathbb{E}[\textrm{math score} | \text{small}_i = 0] &= \mathbb{E}[b_0 + \delta \text{small}_i + e_i | \text{small}_i = 0] \\ &= b_0 + \delta \mathbb{E}[\text{small}_i| \text{small}_i = 0] + \mathbb{E}[e_i|\text{small}_i = 0] \\ &= b_0 \end{align} \]

📌 소규모 학급(처리군, \(small_i = 1\))에서의 기대값 \[ \begin{align} \mathbb{E}[\textrm{math score} | \text{small}_i = 1] &= \mathbb{E}[b_0 + \delta \text{small}_i + e_i | \text{small}_i = 1] \\ &= b_0 + \delta \mathbb{E}[\text{small}_i| \text{small}_i = 1] + \mathbb{E}[e_i|\text{small}_i = 1] \\ &= b_0 + \delta \end{align} \]

📌 평균 처치 효과 (ATE) 계산 \[ \begin{align} ATE &= \mathbb{E}[\textrm{math score} | \text{small}_i = 1] - \mathbb{E}[\textrm{math score} | \text{small}_i = 0] \\ &= b_0 + \delta - b_0 \\ &= \delta \end{align} \]

✅ 이미 알고 있었지만, 이제 이 결과가 왜 성립하는지 공식적으로 이해할 수 있음! 🎉

Task 3

10:00

  1. 아래 코드를 실행하여 1학년(grade == “1”)이며, 일반 학급(regular) 또는 소규모 학급(small)에 속한 학생들만 선택.
star_df_clean <- star_df %>%
    filter(grade == "1" & star %in% c("small", "regular"))
  1. 두 그룹의 평균 수학 점수 및 차이 계산 (Base R 사용)
  1. 더미 변수 생성: 소규모 학급(small) = 1 (TRUE), 일반 학급(regular) = 0 (FALSE) 힌트: treatment = (star == "small").

📈 4. 회귀 분석 실행

❓ 5. 결과 해석: 회귀 분석 결과가 2번 질문에서 구한 평균 차이와 일치하는가?

RCT의 한계

✅ RCTs는 강력한 내부 타당성(Internal Validity)을 가지며, 인과관계를 명확히 확인할 수 있음. 하지만 몇 가지 중요한 한계점이 존재함.

  • ⚠️ 1. RCT 실행의 어려움
    • RCT는 종종 실행이 불가능함.
      • 🏦 비용 문제, 윤리적 문제, 시간 제약
  • 🔍 2. 결과 해석의 어려움
    • 🌍 외부 타당성(External Validity):
      • 특정 RCT의 결과가 다른 국가, 인구집단 등으로 일반화 가능할까?
      • 연구 대상이 제한적이면 다른 환경에서도 같은 결과가 나올까?
    • 🔬 메커니즘 분석의 어려움:
      • 어떤 메커니즘이 작동했는지 분석하는 것이 어려울 수 있음
    • 🎲 완벽하지 않은 무작위 배정
      • 실제 RCT에서는 완전한 랜덤화가 어렵고, 이탈(Attrition) 문제가 발생할 수 있음

✅ RCT는 인과관계를 분석하는 강력한 도구지만, 한계를 이해하고 보완할 필요가 있음! 🎯

🚀 앞으로 배울 내용

✅ RCT에 의존할 수 없다면?
- 우리는 실험 데이터(Experimental Data) 가 아닌, 관측 데이터(Observational Data) 를 이용하여 인과 추론(Causal Inference) 을 수행할 수 있음.

📌 두 가지 주요한 경우

  • ✅ 선택이 관측 가능한 특성(Observable Characteristics)에서 발생하는 경우
    • 다중 회귀(Multiple Regression)
  • ⚠️ 선택이 관측 불가능한 특성(Unobservable Characteristics)에서 발생하는 경우
    • 회귀 불연속 설계(Regression Discontinuity Design, RDD) → Optional
    • 이중 차분법(Difference-in-Differences, DID) → Optional

🔍 인과 관계를 찾아가는 길

✅ 데이터를 어떻게 다룰까? : 읽기(Read), 정리(Tidy), 시각화(Visualize)…

🚧 변수간 관계를 어떻게 요약할까? …단순 선형 회귀(Simple Linear Regression) …계속 학습

✅ 인과 관계(Causality)란 무엇인가?

❌ 전체 모집단을 관측하지 못하면 어떻게 할까?

❌ 우리의 연구 결과가 단순한 무작위(Randomness) 때문일 수도 있을까?

❌ 실제로 외생성을 어떻게 찾아낼 수 있을까?

THE END!

Appendix

처리 집단과 통제 집단에서의 평균 처치 효과 (Average Treatment on the Treated and on the Untreated)

다른 조건부(Conditional) 평균 처치 효과도 중요할 수 있음.

📌 처리 집단에서의 평균 처치 효과 (ATT) (Average Treatment on the Treated, ATT)

\[ \begin{align} ATT &= \mathop{\mathbb{E}}(\delta_i | D_i = 1) \\ &= \mathop{\mathbb{E}}(Y_i^1 - Y_i^0 | D_i = 1) \\ &= \mathop{\mathbb{E}}(Y_i^1 | D_i = 1) - \mathop{\mathbb{E}}(Y_i^0 | D_i = 1) \end{align} \]

  • ATT는 처치 그룹(Treatment Group)에 속한 개인들의 평균 처치 효과를 측정함.
  • 예제: 직업 훈련 프로그램(처치)을 받은 사람들에게 미치는 효과 (처치 그룹 내에서 평가).

📌 통제 집단에서의 평균 처치 효과 (ATU) (Average Treatment on the Untreated, ATU)

\[ \begin{align} ATU &= \mathop{\mathbb{E}}(\delta_i | D_i = 0) \\ &= \mathop{\mathbb{E}}(Y_i^1 - Y_i^0 | D_i = 0) \\ &= \mathop{\mathbb{E}}(Y_i^1 | D_i = 0) - \mathop{\mathbb{E}}(Y_i^0 | D_i = 0) \end{align} \]

  • ATU는 통제 그룹(Control Group)에 속한 개인들이 처치를 받았을 경우의 평균 처치 효과를 측정함.
  • 예제: 사립학교(처치)에 다니는 것이 공립학교 학생(통제 그룹)에게 미칠 효과를 추정.

📌 중요: 대부분의 경우, ATE ≠ ATT ≠ ATU!

🔙 이전으로 돌아가기

단순 비교의 문제점

처치 효과가 모든 개인에게 동일하다는 가정을 완화해 보자.
수식을 전개하면 다음과 같은 형태로 SDO(Simple Difference in Outcomes)를 분해할 수 있음:

\[ \begin{align} SDO &= ATE + \underbrace{\mathop{\mathbb{E}}(Y_i^0 | D_i = 1) - \mathop{\mathbb{E}}(Y_i^0 | D_i = 0)}_\text{Selection bias} \\ & \quad \quad \quad \quad + \underbrace{(1-\pi)(ATT - ATU)}_\text{Heterogeneous treatment effect bias} \end{align} \]

여기서 \(1 - \pi\)는 통제 그룹(Control Group)의 비율을 의미함.

📌 새로운 편향 요소: 개인별 처치 효과의 이질성 (Heterogeneity)

1️⃣ 선택 편향(Selection Bias):
- 대학에 진학하는 학생들은 기본적인 인지 능력이 더 높을 가능성이 높음 (대학 여부와 관계없이).
2️⃣ 이질적 처치 효과 편향(Heterogeneous Treatment Effect Bias):
- 대학에 가는 학생들이 대학에서 더 많은 학습 효과를 얻을 가능성이 높음 (더 동기 부여된 학생들일 수 있음).

🔙 이전으로 돌아가기